[Mascocó]

Antes que nada mi mayor agradecimiento a Tropelio por sus, como siempre, pedagógicas y claras explicaciones. Y también por el trabajo que se toma para hacernos avanzar en estos temas.

También mis disculpas a todos por retomar el hilo tan tarde, pero no he podido profundizar en él hasta hace unos días.

La verdad es que este asunto de calcular nuestra posición a partir de dos observaciones pudiendo prescindir de una situación de estima siquiera aproximada resulta bastante apetitoso. Lo que me parece que puede resultar tedioso es la realización de los cálculos y dibujos sucesivos en el caso de hacerlo por iteraciones o el resolver tres triángulos esféricos en el caso del método de circulos de altura que nos ha explicado tan bien Tropelio al comienzo del hilo.

Por esto me puse a meter los cálculos para las rectas de altura en una hoja de cálculo, también por curiosidad de experimentar cuántas aproximaciones sucesivas serían necesarias para llegar a una buena situación calculada en función de nuestra situación de estima inicial.

A continuación trataré de explicar los resultados obtenidos para algunas situaciones de observación.

Para las observaciones propuestas en el ejemplo de Tropelio de Aldebarán y Hamal, los datos utilizados son los siguientes:



Los datos de entrada a la hoja de cálculo son los de altura verdadera y los astronómicos correspondientes a cada astro. Los de fecha y hora son solo informativos y los de la columna de situaciones de iteración son las dos posiciones a las que se ve que convergen los cálculos, la primera es la supuesta real, que llamaremos So1 (y que naturalmente coincide con la calculada por el método de circulos de altura iguales en el ejemplo de Tropelio), la otra, So2, el otro punto de corte de los círculos de altura.

En la figura siguiente se muestran, resumidos, los resultados de los cálculos sucesivos del cruce de las rectas de altura, no hay más que introducir una situación de estima (cuadros con fondo verde), en principio cualquiera, aquí para le=30ºN,Le=010ºW:



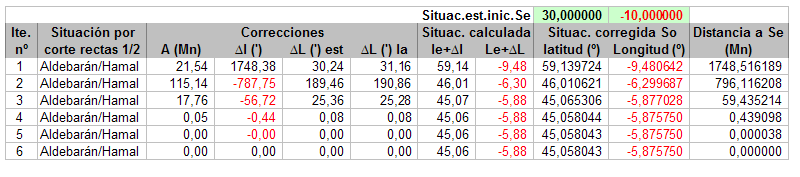Como se ve, al menos para esta situación de estima, converge bastante rápido, bastan tres iteraciones para obtener una situación muy aproximada. A partir de la 6ª va cambiando el dígito menos significativo (de los 15 con los que entiendo trabaja Excel) con una distancia a la situación de estima anterior que, aunque no llega a cero, está en el orden de la billonésima de milla.

Se utilizan dos hojas de cálculo auxiliares para los determinantes de cada iteración. Para este caso concreto:




Probando varias situaciones de estima se obtiene pronto el otro punto de convergencia, aquí para le=30ºS,Le=010ºE:





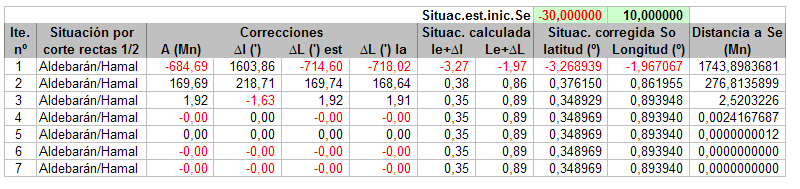Pero hay casos de situación inicial de estima, sobre todo con este ejemplo de observación, en las que hace falta realizar muchas más iteraciones, aunque finalmente termine convergiendo:




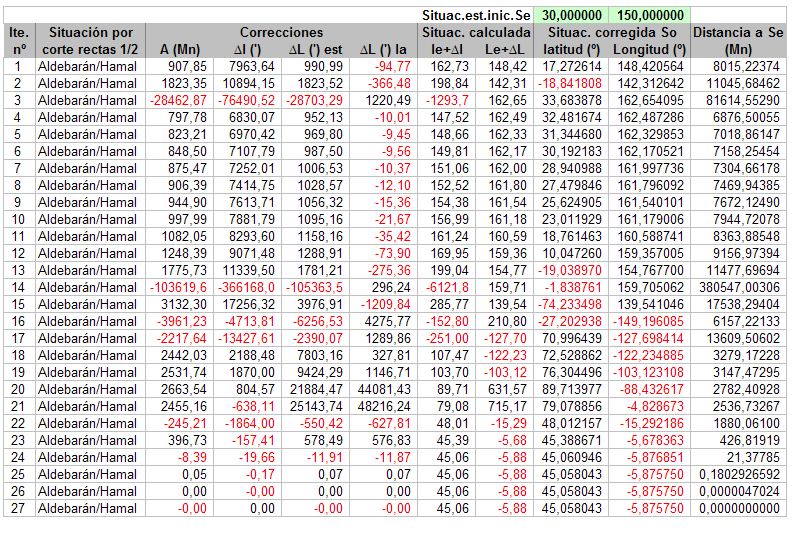Aprovecho éste último caso para explicar alguna de las situaciones que he contemplado al realizar la hoja de cálculo.

Como se puede ver, en varias iteraciones, como en casi todas las primeras, la nº 16 por ejemplo, los valores de de las correcciones obtenidos son un tanto disparatados. Imagino que claramente se debe a que estamos aproximando los círculos de altura por rectas. Para compensar los resultados de latitud y longitud fuera del rango +/-90º y +/-180º respectivamente, los convierto a dentro del rango, (de “Situac. calculada” a “Situac. Corregida So”) de manera que, por ejemplo, lat. +100º -> lat. +80º y Long. -190º -> Long. +170º. No estoy completamente seguro de la corrección de esta conversión para el caso de las latitudes, pero aunque una latitud de -220º no tiene mayor efecto sobre la hoja de cálculo y converge igualmente, molesta verlo.

Otra cosa que se tiene en cuenta, aunque no tiene mayores efectos sobre el nº de iteraciones necesario para un caso dado, es calcular el ∆L por latitudes aumentadas, en lugar de por cálculos de estima, cuando la distancia entre las últimas Se y So es mayor de 300 millas.

También se tiene en cuenta cuando una de las rectas pasa por el punto de Se (∆a=0).




Sigo en otro post.