[Mascocó]

Como lo prometido es deuda, aunque con un poco de retraso, MasBarco ataca de nuevo.

Pués bien, como la cuestión de las iteraciones no me convencía demasiado con la historia de los puntos de no convergencia, o los que pueden necesitar 25 o más iteraciones (imaginaros los cálculos con calculadora), y el método de Círculos de altura iguales tiene el aliciente de que, en principio, no se necesita ninguna situación de estima, he hecho el mismo trabajo que para las iteraciones, es decir meter los cálculos necesarios en una hoja de cálculo para que ésta nos ahorre el trabajo de resolver manualmente (con ayuda de calculadora se supone) los tres triángulos esféricos.

Siguiendo las sumamente claras explicaciones de Tropelio, ésta es la hoja de cálculo que sigue su metodología:



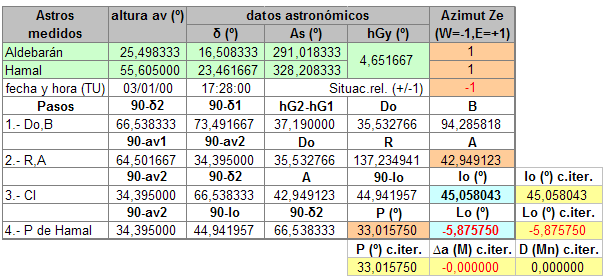Esta hoja es bastante sencilla, mucho más que la de iteraciones, en las que hay que calcular el cruce de dos rectas, apartamientos etc…, aunque luego se complica un tanto si queremos automatizar al máximo la obtención de resultados.

Al igual que en el caso de las iteraciones, basta en principio con introducir los datos astronómicos y la altura verdadera de los astros observados (recuadros en verde). Luego explicaré qué son los datos de la columna de azimut. Los resultados de posición aparecen con fondo azul y el ángulo en el polo obtenido corresponderá al astro que tomamos como “Astro2”, el de la segunda fila de datos.

Las filas y columnas en amarillo en realidad no forman parte de la hoja de cálculo para los círculos de altura, corresponden a los resultados de iteración para una situación de estima aproximada (+1º el lat. y Lon.) a la obtenida por el método de círculos de altura.

En este caso del ejemplo de Aldebarán/Hamal que puso Tropelio, como se puede ver, se obtiene el mismo resultado que en su cálculo y también el mismo que por el método de iteraciones.

Pero veamos qué pasa si aplicamos tal cual estas fórmulas a una de las otras observaciones que hemos tratado en las iteraciones, concretamente a la de Mimosa y Denébola:



Como se puede ver, el resultado no corresponde a ninguno de los dos posibles puntos de observación, mientras que el resultado por el método de iteración converge a la primera de las dos posibles situaciones de observación.

La razón es bien sencilla, el método de cálculo no se puede aplicar a ojos cerrados ya que el cálculo del ángulo A y el signo del ángulo en el polo P dependen de nuestra situación relativa respecto a los dos astros observados.



Continúo en el siguiente post.