 Re: Catenaria y fondeo
Re: Catenaria y fondeo
Las fórmulas.
Con ayuda de esa página, aplicándolo a nuestro caso y a nuestra nomenclatura tenemos lo siguiente:
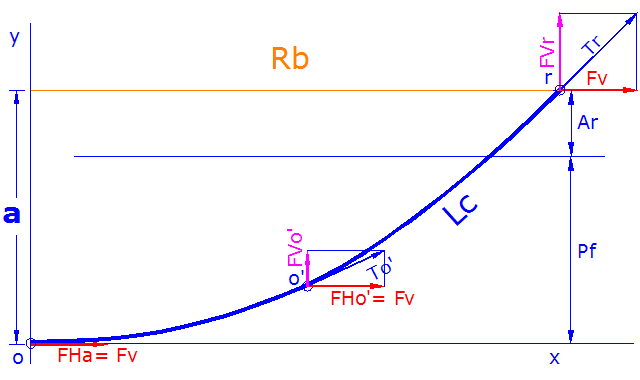
fig.01
Como vereis, tomamos la mitad derecha de la catenaria:
- o es el origen de coordenadas, nuestro punto de anclaje, el más bajo de la catenaria.
- r es el punto desde donde largamos la cadena, suponemos que sea la roldana.
- Lc la longitud de cadena largada, la mitad de longitud de una catenaria completa.
- Rb el radio de borneo, coincide con la mitad de la luz, entre anclajes, de una catenaria completa.
- a es la altura, o flecha, de la catenaria, será la suma de la profundidad Pf y la distancia de la roldana al nivel del mar Ar, a= Pf+Ar.
- Fv es la fuerza, horizontal, que ejerce el viento sobre la embarcación, será siempre igual a lo largo de la catenaria, es decir Fv= FHa, fuerza horizontal sobre el ancla, que a su vez concide con la tensión de la cadena en su unión al ancla.
- FVr es la fuerza, vertical, que ejerce la cadena sobre la roldana.
- Tr es la tensión de la cadena a la salida de la roldana.
- p el peso unitario de la cadena por unidad de longitud.
- Pc el peso total de la cadena largada
La ecuación de la curva catenaria formada por la cadena se puede establecer como:
y= (Fv/p).[cosh(p.x/Fv)-1]
su derivada y’= sinh(p.x/Fv) nos daría la pendiente en el punto, con lo que podríamos calcular la tensión en cada punto.
Para lo que nos interesa se pueden establecer las siguientes ecuaciones:
Fv= (p/2a).(Lc²-a²)
Rb= (Fv/p).asinh(p.Lc/Fv)
Lc= (Fv/p)sinh(p.Rb/Fv)
a= (Fv/p)[cosh(p.Rb/Fv)-1]
FVr= p.Lc= Pc
Tr²= Fv²+Pc²
Evidentemente estas ecuaciones son válidas para “medias catenarias completas” que serán todas las que vaya formando la longitud de cadena que no repose en el fondo, justo hasta el momento en que toda la cadena haya despegado del fondo.
Para centrar ideas me permito recordar rápidamente lo que sucede a nivel de la curva que forma la cadena cuando fondeamos.
Vamos a suponer que no hay corriente ni olas, una vez fondeado el ancla damos atrás para extender la cadena, que el ancla agarre etc… , paramos motor.
- Ahora supongamos que no hay viento, el peso de la cadena llevará el barco hasta que la línea de fondeo quede en vertical, el resto de la cadena (Lc-a) reposa extendida en el fondo.
- Aumenta un poco el viento, el barco se desplaza en su dirección y parte de la cadena que estaba en el fondo se levanta formando una curva catenaria hasta que se igualan las fuerzas y el barco se detiene. El origen de coordenadas que hemos definido en el dibujo de la curva será en este momento, no el punto de anclaje sino justo el punto en que la cadena se levanta del fondo.
- Aumenta más el viento, se repite la situación anterior levantándose más cadena de la que todavía reposaba en el fondo. Se forma otra catenaria distinta a la anterior, de mayor longitud de cadena, igual altura. Cada vez hay menos cadena en el fondo.
- Si sigue aumentando el viento llegará un momento en que justo toda la cadena está levantada del fondo, a la catenaria que forma la cadena en este momento es a la que en adelante llamaré catenaria límite, porque es la de máxima longitud que cumple las ecuaciones de media catenaria que hemos visto.
La fuerza que ejerce el viento, suponemos sólo horizontal, es exactamente la misma transmitida al conjunto “cadena en el fondo”+ancla y en el caso de catenaria límite toda la fuerza del viento es soportada directamente por el ancla, que supondremos que no garrea. Es importante darse cuenta de que hasta este momento sobre el conjunto “cadena en el fondo”+ancla o, en el caso límite directamente sobre el ancla, la fuerza vertical es cero. Creo que ya se intuye con facilidad que el motivo es que la tangente en el punto más bajo de una catenaria es horizontal, pendiente cero, con lo que la tensión en ese punto coincide con la componente horizontal de la fuerza. Hasta aquí estamos en la zona ideal de trabajo de nuestro fondeo ya que, aún suponiendo que el ancla se deslize inicialmente, la dirección de la fuerza aplicada al ancla, solo horizontal, tenderá a enterrar más el ancla en el fondo, si no lo estaba suficientemente y su diseño lo permite, hasta que ya no garrea más que es el supuesto que hacemos.
Cualquier fuerza de viento superior a la que justo hace levantar toda la cadena del fondo, es decir, a la necesaria para formar la catenaria límite, generará una componente vertical distinta de cero y aplicada directamente al ancla, con la consiguiente posibilidad de desenterrarla del fondo, en el peor de los casos hasta que se produzca el garreo. Ahora, la curva que dibuja nuestra cadena sería la de un arco de catenaria, a la que ya no se aplicarían directamente nuestras ecuaciones. Esta curva sería, por ejemplo en el caso de la figura, el arco catenario desde el punto o’ hasta r de longitud Lc la de la cadena que teníamos largada y distancia vertical a r la misma altura a que teníamos inicialmente, lo que habrá disminuído será el radio de borneo Rb, es decir, ahora nuestro ancla estaría en el punto o’ y la fuerza vertical sobre la misma, FVo’ ya no sería cero. La nueva catenaria que define la curva de nuestra cadena sería otra con una nueva altura, una nueva longitud y un nuevo radio de borneo. Así, es posible determinar la nueva catenaria por procedimientos iterativos de aproximación, lo que nos permitiría calcular la pendiente en el punto o’ y de ahí la FVo’, pero en realidad, aparte de que esto se sale de mis pretensiones, creo que se puede afirmar que enseguida, con poco incremento de fuerza del viento, la pendiente se va a aproximar a la recta desde el punto de anclaje a la roldana con lo que la fuerza vertical sobre el ancla FVo’ ya la podemos calcular directamente según la relación de fondeo Lc/a.
… 
|