[Mascocó]

Pesos en el fondo.

Veamos ahora qué ocurre a nivel de pesos utilizando cadena de 8 o de 10 mm. Vistas las conclusiones anteriores sobre la mayor importancia de la longitud respecto al peso vamos a suponer que aunque cambiemos de cadena vamos a conservar la misma longitud, para nuestro caso 60 m.

Estudiando el peso de cadena que reposa en el fondo obtenemos las siguientes curvas para una altura de 5 metros y una relación, en principio, de 5:1.

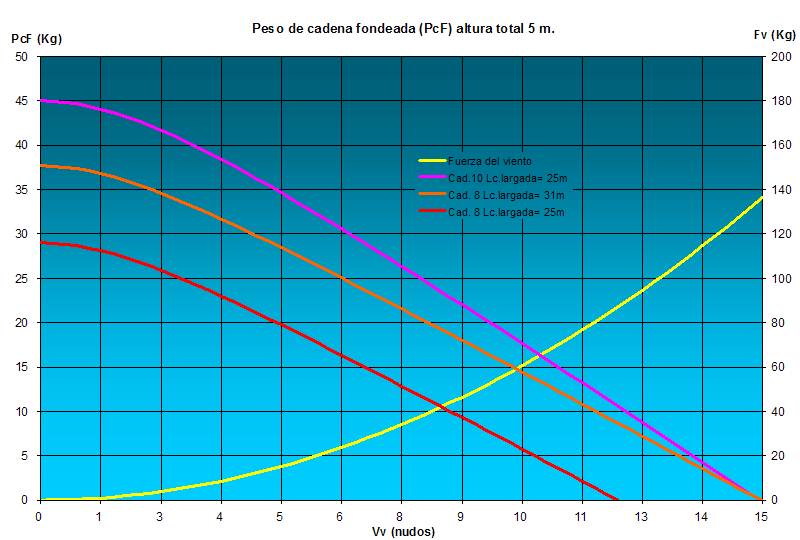
fig.12

Como se ve, el peso de cadena en el fondo va disminuyendo desde los 45 Kg para cadena de 10 mm o de 29 Kg para la cadena de 8 mm hasta cero, cuando se forma la catenaria límite. La diferencia de prestaciones para un diámetro u otro se reduce al final en la fuerza de viento necesaria para levantar toda la cadena del fondo, 15 nudos y 12 nudos en cada caso. He añadido una tercera curva para la cadena de 8 mm, aumentando su longitud hasta 31 m para obtener las mismas prestaciones que con la cadena de 10 mm en la que se puede ver que lógicamente el peso en el fondo varía ahora desde los aproximadamente 38 Kg iniciales hasta cero, en este caso para la misma fuerza de viento que para la cadena de 10 mm, 15 nudos.

He considerado la cadena como si fuera un cable completamente flexible del mismo peso por unidad de longitud, ya que la cadena está compuesta por eslabones de un determinado tamaño la situación real no es exactamente esta, ya que la cadena se va levantando eslabón por eslabón por así decir, cada uno con un cierto ángulo con la horizontal, pero, para todos los efectos considero que la aproximación tomada es suficientemente válida.

Las curvas están dibujadas calculando la longitud de catenaria para cada fuerza de viento, esa longitud, restada a la total de cadena que hemos largado nos da la que permanece reposando en el fondo y por tanto el peso.

Cada fuerza de viento será igual a la suma de la fuerza de rozamiento estática del trozo de cadena en el fondo y la resistencia a la tracción horizontal del ancla. En principio he supuesto que partimos de una cadena estirada pero en el fondo creo que dará igual, al final habrá una cierta longitud de cadena fuera del fondo para igualar cada fuerza de viento, si la cadena no estaba estirada habrá habido, digamos, un balanceo hasta el equilibrio, pero finalmente se llegará a él. En este último caso habrá una fuerza de rozamiento estático y otra dinámica hasta llegar al equilibrio pero es esta última situación la que nos interesa.

Esto último me lleva a reflexionar sobre algo que muchas veces se dice, algo así como que lo importante en un fondeo es que no trabaje el ancla. Bueno, todos podemos estar de acuerdo con esto, si no trabaja el ancla quiere decir que no ejercemos ninguna fuerza sobre ella, con lo que dificilmente va a garrear y nuestro fondeo será cien por cien seguro, pero ¿puede darse este caso?, pues si, pero solamente mientras la fuerza de rozamiento estático del conjunto de cadena que reposa en el fondo sea superior a la del viento.

Para poder calcular la máxima fuerza de rozamiento de la cadena en el fondo necesitaríamos conocer el coeficiente de rozamiento estático de la cadena con el fondo, éste coeficiente evidentemente variará ampliamente según la naturaleza del fondo y además también la fuerza de rozamiento variará con la inclinación del fondo, pero para hacernos una idea voy a considerar un fondo plano y un coeficiente de rozamiento estático de u=0,6. Este coeficiente corresponde al estático para acero/hormigón, lo más aproximado que he podido encontrar, se le suele dar entre 0,5 y 0,65, evidentemente para un fondo de arena será otro, posiblemente mayor, no sabría decirlo. Tendremos entonces, para un u dado:

Frmáx= u.Pcfdo

Como ya he dicho, mientras Frmáx,>Fv el ancla no trabaja, cuando sea menor, la resistencia a la tracción que debe soportar el ancla será:

FHa= Fv- Frmáx = Fv-u.Pcfdo

Con esto podemos dibujar las siguientes curvas, otra vez para una altura de 5 m y relación de fondeo 5:1.

fig.13

He vuelto a dibujar una tercera curva para la cadena de 8 mm para 31m de cadena largada para igualar la fuerza necesaria para la catenaria límite, al igual que en las gráficas anteriores. Como era de esperar esta curva y la de la cadena de 10 mm son muy similares.

A partir de unos 5 nudos de viento comienza a haber tracción sobre el ancla, pequeña al principio y siempre menor que la del viento pero que se aproxima a ésta rápidamente, ya para 10 nudos con fuerza de viento 60 Kg, la fuerza, solo horizontal, sobre el ancla es de 57 Kg con la cadena de 8 mm y de 50 Kg con la de 10 mm. En la cadena de 8 mm, relación 5:1 la curva, al llegar a los 12 nudos (formación de la catenaria límite), se confunde con la del viento, a partir de aquí como ya sabemos habrá componente vertical actuando sobre el ancla.

…