[Mascocó]

A vueltas con el viento que importa.

Han pasado tres semanas desde mi último post, mucho tiempo, con lo que quizás ya tengais este tema completamente olvidado. Aún así, como creo que quedaban un par de cosas por intentar definir un poco mejor y no quería dejarlo sin terminar, aquí estoy de nuevo.

Como creo que ya dije, pensaba atacar la cuestión desde dos aspectos, por un lado la fuerza base sobre el barco y por otro incluir en los cálculos una cierta angulación en la tracción del ancla para tratar de llegar a resultados más cercanos a lo que ocurre realmente en el fondeo.

Respecto a la fuerza base a su vez había dos cuestiones entrelazadas, por un lado la magnitud de la fuerza en sí, y por otro la variación de ésta considerando la disminución de la velocidad del viento con la altura. Respecto a ésta última habíamos visto que, según lo explicado en la página de Alain Fraysse (AF en lo sucesivo), considerando esa variación tendríamos fuerzas del orden de la tercera parte del valor que saldría considerando constante el viento estándar a 10 m y menos todavía para la normalmente mayor altura de medición, lo que vendría a explicar la diferencia entre las tablas de la ABYC y los valores experimentales o los calculados según superficies al viento.

En principio esta explicación parecía razonable pero, profundizando en ella le encuentro un par de inconvenientes, primero porque este razonamiento también sería aplicable a los propios resultados teóricos obtenidos por el propio AF (que considera velocidad constante a lo largo de la altura de interés) y segundo porque la reducción de la fuerza no llega al 33% sino escasamente al 60% y no en todos los casos. Respecto a esto último, una reducción en velocidad de viento del 71% implicaría una reducción en fuerza del 50%, AF habla de reducciones medias en velocidad para las alturas de interés del orden del 80% lo que en principio no es consecuente con esto, pero pensé que calculando la fuerza integrando la velocidad a lo largo de la altura y las superficies de interés se llegaría a esa reducción mencionada a la tercera parte de la fuerza, pero no es así. Por ejemplo, aunque los resultados varían ligeramente según el perfil de viento elegido (que veremos más adelante), con los datos de superficies y coeficientes aerodinámicos obtenidas por AF para el velero de 40’ a 30º del eje del viento (suponiendo 1,8 m para la obra muerta y 17 m altura del sensor), realizando la integración resulta una disminución de la fuerza sobre el barco a 20 nudos del 60% y para el yate de motor (4 m de cubierta y viento estándar a 10 m) del 68%.

Así que lo que he tratado de hacer es buscar un método para aplicar esta reducción. Básicamente hay dos fórmulas para considerar la variación del viento con la altura, el perfil de viento, una que llamaremos exponencial y la otra logarítmica. La fórmula exponencial es relativamente sencilla pero no tiene en cuenta la propia velocidad del viento, es la siguiente:

v(h)=vr.(h/hr)^α
v(h)= velocidad del viento a la altura h
vr= velocidad del viento a la altura hr
α= constante de Hellmann

el valor de α normalmente dado para superficies de agua planas es de α=0,14 aunque parece más adecuado considerarlo como α=0,11 para la superficie del mar.

La otra fórmula, la logarítmica, es la siguiente:

u(z)= u*/k.Ln(z/z0)
u(z)= velocidad del viento a la altura z
u*= velocidad de fricción
k= 0,42 (constante de Karman)
z0= altura de rugosidad (donde el viento se hace nulo)

No quisiera extenderme mucho en esto y además los cálculos para u* y z0 varían de unos autores a otros e incluso con los mismos métodos se aplican coeficientes diferentes, además para nuestro caso disponemos de una velocidad de referencia medida a una cierta altura, con lo que la fórmula logarítmica la podemos expresar como:

v(h)= vr. Ln(h/z0)/Ln(hr/z0)

quedándonos por tanto, conocidas vr y hr, solamente por definir la altura de rugosidad z0. Lo más aplicable que he encontrado a nuestro caso, superficie del mar y régimen turbulento en el margen de velocidades de interés, utiliza la fórmula de Charnock para expresar z0 que no reproduciré pero que en resumen viene a relacionar z0 con la velocidad del viento para un margen de entre 4 y 50 m/s (aprox. 8-100 nudos), resultando para 10 m de altura un z0 de 0,1 mm para 5 m/s y de 1 mm para 10 m/s, lo que resulta consecuente con los valores normalmente encontrados de z0= 0,0002 a 0,0003.

Para ver la influencia de estos dos modos de calcular el perfil de viento en la fuerza final resultante sobre el barco he dibujado sus curvas:

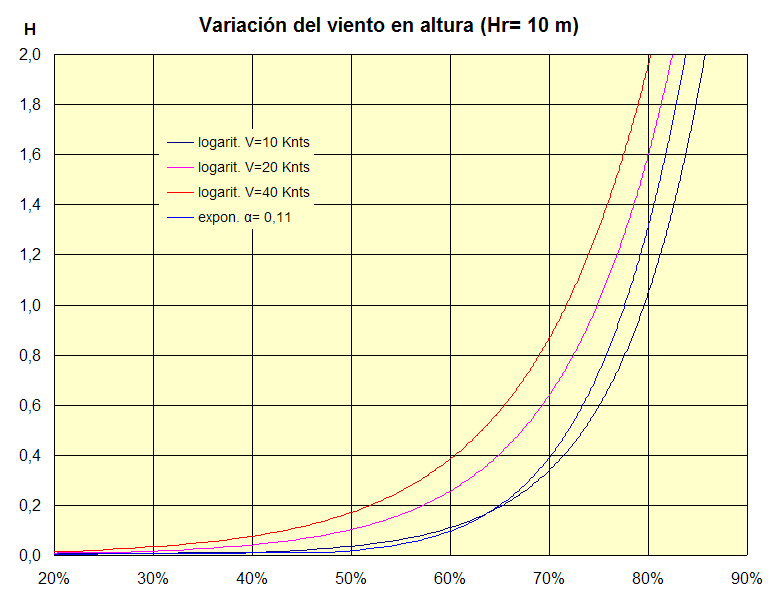
fig.31

Estan representadas las curvas según la fórmula exponencial (en azul), que no varía con la velocidad y la logarítmica para tres velocidades de viento, 10, 20 y 40 nudos. He reducido los márgenes a la altura, 0 a 2 m, de mayor interés para nuestro caso aunque para alturas mayores se puede ver la tendencia.

Se puede observar que el perfil de viento que representa la curva exponencial esta más o menos entre las de 10 y 20 nudos del logarítmico, con el que la velocidad de viento disminuye con la altura en mayor medida cuando aumenta la velocidad de viento, es principio es de esperar que la curva logarítmica se acerque más al perfil real, aunque tampoco hay diferencias fundamentales.

Bueno, ya no me voy a extender mucho más, el resumen es que después de observar el comportamiento de estas curvas integrando a lo largo de las alturas de interés para las superficies de los ejemplos supuestos de AF, como no vamos a disponer de esos datos para cada barco en concreto, he terminado deduciendo una generalización con la que se puede establecer una correlación entre la relación fuerza compensada/sin compensar y la de velocidades del viento v(h)/vr a una determinada altura, siendo para perfil logarítmico h= 20% de la altura de la obra muerta, con un porcentaje de error por debajo del 5% y siempre menor del 10% para casos extremos de yate de motor. Esto igualmente es aplicable para el perfil exponencial (con h= 9% de la cubierta) con un error poco mayor pero más variable con la velocidad de viento, así que he preferido utilizar la fórmula logarítmica a pesar de obligar a calcular un z0 para cada velocidad de viento aunque realmente, con todos los supuestos asumidos, lo mismo daría utilizar un perfil u otro.

Aplicando este sistema conseguiríamos una compensación de la influencia de la variación del viento en altura en la reducción de la fuerza para obtener una más aproximada a la correspondiente al mayor viento medido a mayor altura. Evidentemente no pretendo con esto obtener más que resultados aproximados, de hecho todos los datos que he utilizado para su obtención lo son en sí mismos, sino únicamente tratar de acercarme en lo posible a una situación de cálculo de magnitudes de fuerza más cercanas al caso real.

Entonces, resumiendo, creo que las tablas de la ABYC son en principio adecuadas para su utilización como base de los cálculos, teniendo en cuenta que incluyen efectos sobre el barco que otros métodos no incluyen, como la tendencia del barco a desviarse del eje del viento y algún otro efecto dinámico (aunque no conocemos exactamente cuál ni en qué medida), seguramente estén sobredimensionadas, máxime para algún caso concreto, pero ese factor extra de seguridad creo que debe ser bienvenido. Ahora bien, al mismo tiempo creo que hay que tener en cuenta que medimos el viento a una altura mayor que la de su zona de influencia y corregirlo de alguna manera, que es lo que he tratado de hacer para incorporarlo a la nueva hoja de cálculo que presentaré más adelante.