Catenaria y fondeo

[Mascocó]

Hace un par de semanas, en el transcurso de unas prácticas, uno de nosotros planteó la siguiente cuestión:

¿Me interesa cambiar la cadena de 8 mm. por otra de 10 mm.?.

Pensando en lo que sabía de su barco, velero, algo más de 11 m. de eslora, manga contenida aunque desplazamiento también posiblemente más alto para lo que se estila ahora, mi primera respuesta fué en el sentido de que, si bien ganaría a la hora de fondear iba a perder prestaciones de navegación al aumentar mucho el peso de cadena en el pozo de anclas y que, no necesitándolo imperativamente por el tipo de barco, no le valdría la pena. Otra postura que surgió, en el sentido de que sí le interesaría, decía que siempre podría tener menos longitud de cadena de 10 mm, con lo que se compensarían los pesos y que necesitaría largar menos cadena a la hora de fondear, y también el compensar la menor longitud de cadena con más cabo.

Esto me hizo imaginarme la forma de la curva de una cadena más corta y más tensa y tirando hacia arriba del ancla, así que, recordando el estudio de la catenaria en la Escuela (años ha, muchos jeje) dije que la forma de la curva era siempre una catenaria que dependía de la longitud y no del peso de la cadena, con lo que una cadena más corta tendría necesariamente que tirar del ancla con un ángulo más desfavorable. Pero enseguida me dí cuenta que eso podía ser cierto pero que lo que también iba a hacer una cadena más pesada era acercar el barco al ancla, con lo que, al final, aún siendo más corta la cadena de 10, la curva podía ser la misma, o mejor.

Bueno, la cosa se quedó ahí, tampoco había mucho tiempo para insistir en la discusión. Pero yo me quedé con la mosca detrás de la oreja, por un lado porque no estaba completamente seguro de que lo que había dicho de que a igual longitud igual catenaria fuera exacto y por otro porque seguía con la duda de que se pudiera compensar el peso disminuyendo la longitud, más que nada por la idea de que siempre fondeamos con la relación cadena largada a profundidad.

Así que cuando volví a Madrid y tuve un rato, que al final ha sido un buen rato, me puse a investigar sobre las catenarias y los fondeos en internet y también en la Taberna. Bueno, decir que mi búsqueda de una fórmula aplicable para la catenaria fue bastante infructuosa, mucha ecuación diferencial, integraciones, ejes absolutos y canónicos etc… etc… pero nada que pudiera aplicar fácilmente en nuestro caso de fondeos, algo saqué en claro, al menos, y fué encontrar una demostración matemática de que no podía haber dos curvas catenarias diferentes con la misma longitud y la misma separación entre puntos de anclaje, con lo que efectivamente el peso no entra en la forma. También de paso me he enterado, que Galileo la confundía con la parábola, que hasta finales del XVII no se derivó su ecuación, que Miguel Angel tuvo que reforzar la base de la cúpula de la Capilla Sixtina con una cincha de hierro porque se agrietaba (no era catenaria) y que tuvimos que esperar hasta el siglo XIX para que arquitectos como Gaudí y su contemporáneo, y eclipsado por él, Luis Mancunill, utilizaran las propiedades del arco catenario… mientras que culturas del Islam lo utilizaron mucho antes y los sudaneses construían desde tiempos inmemoriales amplias habitaciones con forma de bóveda catenaria, de adobe, por la escasez de madera.

Pues no encontré nada útil hasta que se me ocurrió buscar catenary y rápidamente encontré esta página donde está todo lo que necesitaba:

http://mysite.du.edu/~jcalvert/math/catenary.htm


Bueno, como esto va a ser largo lo voy a desarrollar en unos cuantos post así que ponéos cómodos y algo de beber, que pago yo.

…

[Mascocó]

Las fórmulas.

Con ayuda de esa página, aplicándolo a nuestro caso y a nuestra nomenclatura tenemos lo siguiente: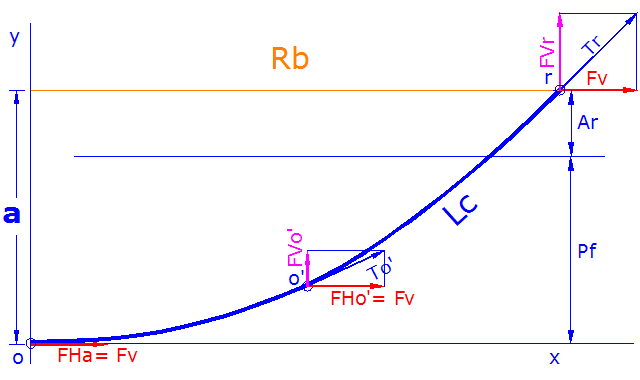

fig.01

Como vereis, tomamos la mitad derecha de la catenaria:

- o es el origen de coordenadas, nuestro punto de anclaje, el más bajo de la catenaria.
- r es el punto desde donde largamos la cadena, suponemos que sea la roldana.
- Lc la longitud de cadena largada, la mitad de longitud de una catenaria completa.
- Rb el radio de borneo, coincide con la mitad de la luz, entre anclajes, de una catenaria completa.
- a es la altura, o flecha, de la catenaria, será la suma de la profundidad Pf y la distancia de la roldana al nivel del mar Ar, a= Pf+Ar.
- Fv es la fuerza, horizontal, que ejerce el viento sobre la embarcación, será siempre igual a lo largo de la catenaria, es decir Fv= FHa, fuerza horizontal sobre el ancla, que a su vez concide con la tensión de la cadena en su unión al ancla.
- FVr es la fuerza, vertical, que ejerce la cadena sobre la roldana.
- Tr es la tensión de la cadena a la salida de la roldana.
- p el peso unitario de la cadena por unidad de longitud.
- Pc el peso total de la cadena largada

La ecuación de la curva catenaria formada por la cadena se puede establecer como:

y= (Fv/p).[cosh(p.x/Fv)-1]

su derivada y’= sinh(p.x/Fv) nos daría la pendiente en el punto, con lo que podríamos calcular la tensión en cada punto.

Para lo que nos interesa se pueden establecer las siguientes ecuaciones:

Fv= (p/2a).(Lc²-a²)

Rb= (Fv/p).asinh(p.Lc/Fv)

Lc= (Fv/p)sinh(p.Rb/Fv)

a= (Fv/p)[cosh(p.Rb/Fv)-1]

FVr= p.Lc= Pc

Tr²= Fv²+Pc²

Evidentemente estas ecuaciones son válidas para “medias catenarias completas” que serán todas las que vaya formando la longitud de cadena que no repose en el fondo, justo hasta el momento en que toda la cadena haya despegado del fondo.

Para centrar ideas me permito recordar rápidamente lo que sucede a nivel de la curva que forma la cadena cuando fondeamos.

Vamos a suponer que no hay corriente ni olas, una vez fondeado el ancla damos atrás para extender la cadena, que el ancla agarre etc… , paramos motor.

- Ahora supongamos que no hay viento, el peso de la cadena llevará el barco hasta que la línea de fondeo quede en vertical, el resto de la cadena (Lc-a) reposa extendida en el fondo.
- Aumenta un poco el viento, el barco se desplaza en su dirección y parte de la cadena que estaba en el fondo se levanta formando una curva catenaria hasta que se igualan las fuerzas y el barco se detiene. El origen de coordenadas que hemos definido en el dibujo de la curva será en este momento, no el punto de anclaje sino justo el punto en que la cadena se levanta del fondo.
- Aumenta más el viento, se repite la situación anterior levantándose más cadena de la que todavía reposaba en el fondo. Se forma otra catenaria distinta a la anterior, de mayor longitud de cadena, igual altura. Cada vez hay menos cadena en el fondo.
- Si sigue aumentando el viento llegará un momento en que justo toda la cadena está levantada del fondo, a la catenaria que forma la cadena en este momento es a la que en adelante llamaré catenaria límite, porque es la de máxima longitud que cumple las ecuaciones de media catenaria que hemos visto.

La fuerza que ejerce el viento, suponemos sólo horizontal, es exactamente la misma transmitida al conjunto “cadena en el fondo”+ancla y en el caso de catenaria límite toda la fuerza del viento es soportada directamente por el ancla, que supondremos que no garrea. Es importante darse cuenta de que hasta este momento sobre el conjunto “cadena en el fondo”+ancla o, en el caso límite directamente sobre el ancla, la fuerza vertical es cero. Creo que ya se intuye con facilidad que el motivo es que la tangente en el punto más bajo de una catenaria es horizontal, pendiente cero, con lo que la tensión en ese punto coincide con la componente horizontal de la fuerza. Hasta aquí estamos en la zona ideal de trabajo de nuestro fondeo ya que, aún suponiendo que el ancla se deslize inicialmente, la dirección de la fuerza aplicada al ancla, solo horizontal, tenderá a enterrar más el ancla en el fondo, si no lo estaba suficientemente y su diseño lo permite, hasta que ya no garrea más que es el supuesto que hacemos.

Cualquier fuerza de viento superior a la que justo hace levantar toda la cadena del fondo, es decir, a la necesaria para formar la catenaria límite, generará una componente vertical distinta de cero y aplicada directamente al ancla, con la consiguiente posibilidad de desenterrarla del fondo, en el peor de los casos hasta que se produzca el garreo. Ahora, la curva que dibuja nuestra cadena sería la de un arco de catenaria, a la que ya no se aplicarían directamente nuestras ecuaciones. Esta curva sería, por ejemplo en el caso de la figura, el arco catenario desde el punto o’ hasta r de longitud Lc la de la cadena que teníamos largada y distancia vertical a r la misma altura a que teníamos inicialmente, lo que habrá disminuído será el radio de borneo Rb, es decir, ahora nuestro ancla estaría en el punto o’ y la fuerza vertical sobre la misma, FVo’ ya no sería cero. La nueva catenaria que define la curva de nuestra cadena sería otra con una nueva altura, una nueva longitud y un nuevo radio de borneo. Así, es posible determinar la nueva catenaria por procedimientos iterativos de aproximación, lo que nos permitiría calcular la pendiente en el punto o’ y de ahí la FVo’, pero en realidad, aparte de que esto se sale de mis pretensiones, creo que se puede afirmar que enseguida, con poco incremento de fuerza del viento, la pendiente se va a aproximar a la recta desde el punto de anclaje a la roldana con lo que la fuerza vertical sobre el ancla FVo’ ya la podemos calcular directamente según la relación de fondeo Lc/a.

…

[Mascocó]

Un ejemplo de la catenaria en fondeo.

En los siguientes gráficos se representan las curvas para una situación de fondeo con altura total 5 m y relación de fondeo 5:1 es decir largados 25 m de cadena, para distintas velocidades de viento:

Para cadena de 8 mm.: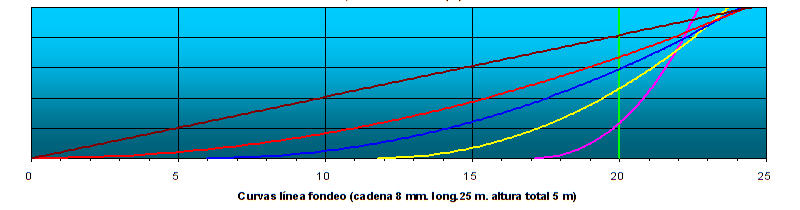

fig.02

Para cadena de 10 mm.: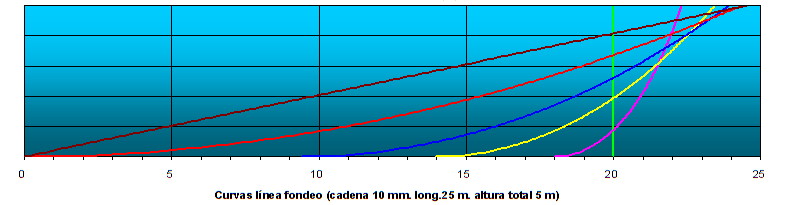

fig.03

Están representadas las curvas para velocidad de viento cero, 3, 6 y 9 nudos y la necesaria para formar la catenaria límite, 12 y 15 nudos para cadena de 8 y 10 mm respectivamente, así como la situación de cadena completamente extendida (por cierto situación imposible de conseguir, ni teórica ni prácticamente, aunque sí sobre el papel. El cuadro resumen de velocidad y fuerza de viento y los radios de borneo es el siguiente: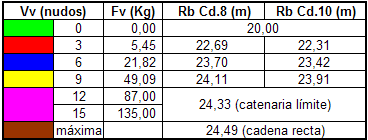

fig.04

Una primera conclusión que se podría sacar de estos resultados es que, a igualdad de metros largados de cadena de 8 y de 10 mm los radios de borneo difieren en poco para una cadena u otra siendo, como ya se había adelantado, exactamente los mismos, e igual curva, para la catenaria límite, con la diferencia de aguantar tres nudos más de viento para obtener ésta en la cadena de 10, que no parece mucho pero que cabía esperar que no lo fuera ya que la influencia del peso es lineal y la de la velocidad del viento cuadrática.


NOTAS:
1.- Estos cálculos, y todos los que siguen, están realizados para la fuerza ejercida por el viento según el cuadro resumen de la ABYC (American Boat and Yacht Council) publicado en el libro de Earl Heinz “The Complete Book of Anchoring & Mooring”. He tomado el dato para eslora 40 pies, 300 libras de fuerza para 15 nudos de viento y extrapolado para otras velocidades según la relación cuadrática consiguiente.
2.- No se tiene en cuenta la influencia de que una parte de la cadena está sobre el agua y el resto sumergida, ni la influencia en ésta última del agua sobre el peso de la cadena, consideraremos entonces el peso unitario de la cadena igual a lo largo de toda su longitud. De esta manera he tomado para todos los cálculos un peso unitario de 1,45 Kg/m para la cadena de 8 mm y de 2,25 Kg/m para la de 10 mm.

…

[Mascocó]

Igualando pesos.

Veamos qué sucede si igualamos pesos de cadena largada, bien sea ésta de 10 mm o de 8 mm. Si tomamos la fórmula para la catenaria límite:

Fv= (p/2a).(Lc²-a²)

vemos que el peso influye linealmente, mientras que la longitud lo hace de manera cuadrática, así que directamente podemos concluir que no podemos disminuir la longitud de la cadena de 10 en relación a su mayor peso respecto a la de 8 y esperar obtener los mismos resultados.

Veamos cuál es esta diferencia:

Si disminuimos la longitud de cadena de 10 respecto a la de 8 para igualar el peso de cadena en el agua o bien aumentamos la longitud de la de 8 en relación a la de 10 y representamos el incremento de fuerza de viento soportada por la cadena de 8 respecto a la de 10, es decir (Fv8/Fv10)-1 nos salen las gráficas siguientes: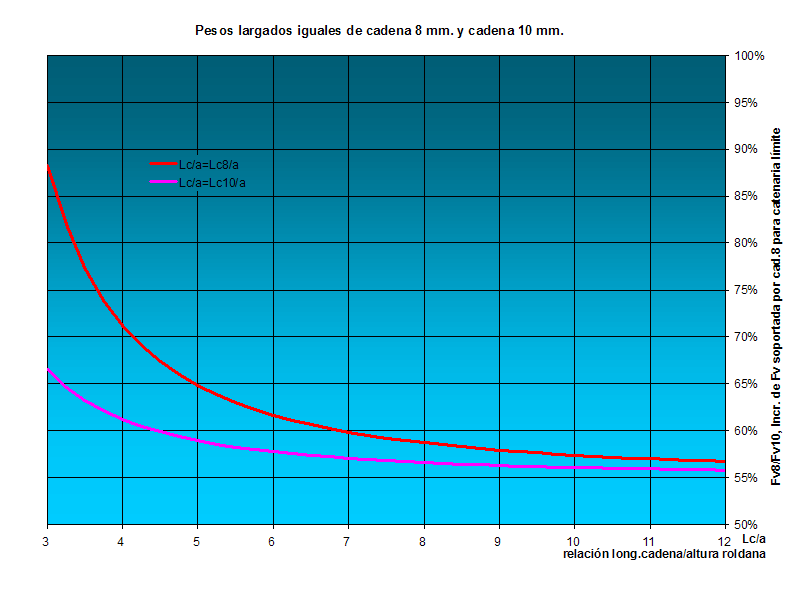

fig.05

Donde se puede ver que, a igualdad de peso en el agua seremos capaces de soportar más fuerza de viento con la cadena de 8 mm que con la de 10 mm, concretamente, para el caso de relación Lc8/a= 5, un 65% más hasta empezar a tirar del ancla en vertical en una u otra cadena.

…

[Mascocó]

Igualando fuerzas.

Visto esto parece claro que un enfoque más razonable sería igualar las fuerzas a soportar por los dos diámetros de cadena y ver qué longitud se necesita en cada caso. Igualando fuerzas podemos obtener las gráficas necesarias para ese cálculo en función de las relaciones Lc/a:

fig.06

Es decir, para obtener las mismas prestaciones con una relación de fondeo de 5:1 de cadena de 8 mm. por ejemplo, nos bastaría con una relación de 4:1 aproximadamente de cadena de 10 mm., es decir, para una altura total de 5 metros y esta relación necesitaríamos 25 m de cadena de 8 y 20 m de 10 (en lugar de los 16 que necesitábamos igualando pesos). Ahora bien, esto es válido hasta que llegamos a la catenaria límite, a partir de aquí una mayor fuerza de viento va a producir, como ya hemos visto, una fuerza vertical sobre el ancla que, aunque inicialmente viene dada por la descomposición de la tensión según la pendiente de la catenaria (ahora un arco de catenaria) en el punto de anclaje, enseguida ésta va a tender a la línea recta hacia la roldana, con lo que lo importante ahora va a ser el ángulo de la cadena con la horizontal. Con esta aproximación, ya que la fuerza vertical será el producto de la fuerza del viento por la tangente del ángulo de la cadena, la relación de fuerzas será FVa10/Fva8=[(52-1)/(42-1)]1/2= 1,265, es decir un 26,5% más de fuerza vertical en el caso de cadena de 10 mm. Para hacernos una idea, la fuerza del viento para 20 nudos es de 242 Kg para el barco que estudiamos, supuesta la cadena tensa se generará una fuerza vertical de 49 Kg en la cadena de 8 mm y de 62 Kg en la de 10 mm. esos 13 Kg más pueden hacer la diferencia para que el ancla comienze a garrear con la cadena de 10 y no con la de 8. Bueno, está claro que en ambos casos ya deberíamos haber soltado más cadena, pero parece claro también que antes con la de 10 mm.

Por último, añadir en cuanto al radio de borneo que más o menos se disminuye en la diferencia de longitudes de cadena, para este caso en unos 5 m con la de 10 mm.

…

[Mascocó]

Las gráficas para distintos fondeos.

Bueno, antes de analizar la cuestión de pesos en el pozo de anclas de una cadena u otra, voy a presentar unas gráficas para algunas alturas de fondeo en particular, más que nada para saber el orden de magnitud de fuerzas con las que tratamos.

En todos los casos se supone que disponemos de hasta 60 metros de cadena con lo que las relaciones de fondeo podrán llegar hasta 12:1 en el caso de 5 m de altura total o solamente a 6:1 en el caso de altura 10 m. Se ha representado la fuerza del viento hasta 30 nudos, que está en el orden de la que se puede aguantar con 60 m de cadena hasta la catenaria límite, al menos en la mayoría de los casos, y además eso permite igualar las escalas para una más fácil lectura del gráfico.

Para una altura total de 5 m la gráfica sería: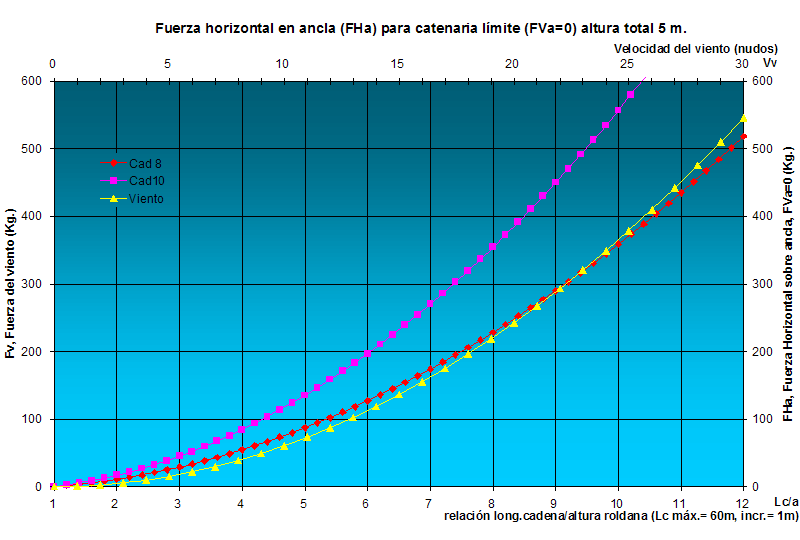

fig.07

La gráfica nos permite conocer la máxima fuerza de viento que podemos aguantar para esa altura, para una cierta relación de fondeo o para una longitud de cadena dada, por ejemplo, si hemos fondeado con 30 m de cadena, relación 6:1, aguantaremos hasta unos 125 Kg de fuerza de viento con cadena de 8 mm y de 200 Kg con cadena de 10 mm, que llevado en horizontal a la curva de viento equivalen a unos 15 y 18 nudos respectivamente. A la inversa, si el viento sube a 20 nudos por ejemplo, necesitariamos 41 m de cadena de 8 mm (8x5+1) ó 33 m de cadena de 10 mm (6x5+3).

A continuación están las gráficas correspondientes a 6, 8 y 10 m de altura total.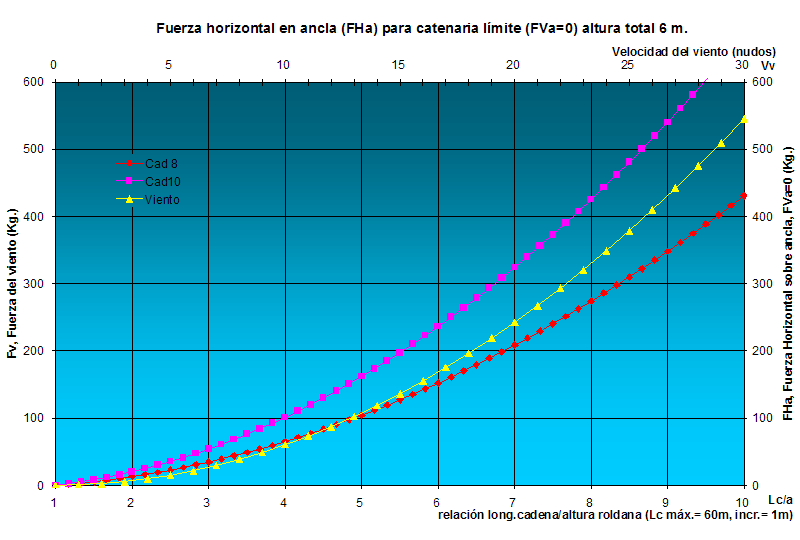

fig.08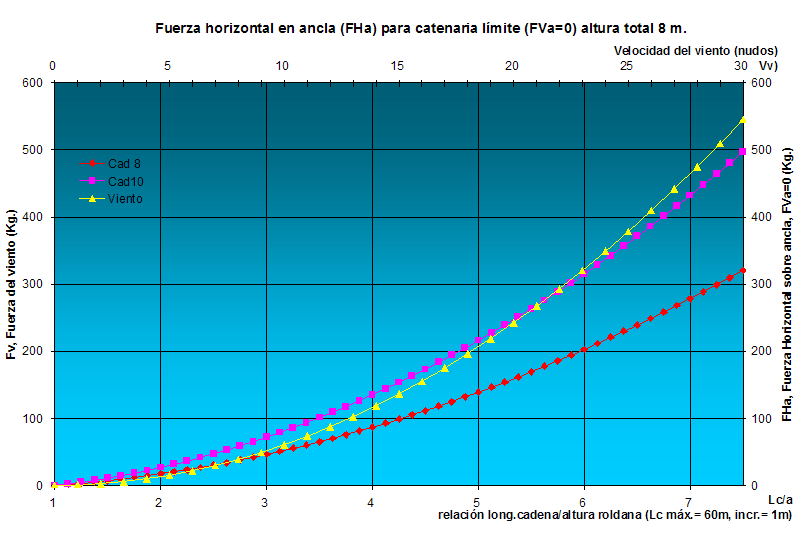

fig.09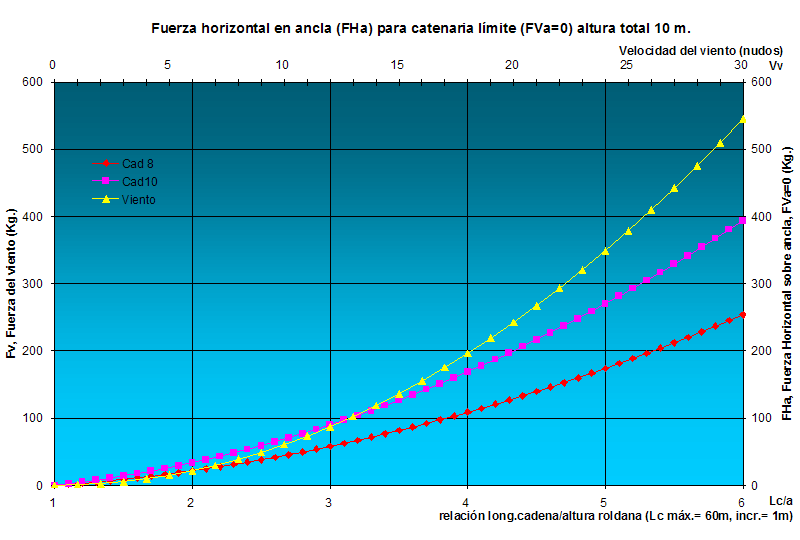

fig.10

Observando estas gráficas para diferentes profundidades se comprende fácilmente por qué a medida que aumenta la profundidad necesitamos comparativamente menos relación de fondeo. Esto se debe a la mayor influencia de la longitud respecto a la altura de la catenaria en el efecto amortiguador de la misma (la longitud influye en un termino al cuadrado mientras que la altura en potencia de uno). Por ejemplo, para altura total de 10 m y relación 6:1 aguantaremos hasta poco menos de 20 y 26 nudos con cadena de 8 y de 10 respectivamente, mientras que la misma relación para altura 5 m. nos da menos de 15 nudos para cadena de 8 y 18 nudos para cadena de 10. Claro, que hemos largado toda la cadena (60 m) en un caso y solo 30 m en el otro, pero para obtener los mismos resultados en el caso de altura 5 m hubiéramos necesitado largar 42 m de cadena de 8 mm o 43 m de cadena de 10 mm. Además, para mayores profundidades es razonable esperar que se forme menos ola y en cualquier caso su influencia relativa será menor, así, podríamos tener una ola de 1 m en el caso de altura 5 m y sólo 0,5 m en altura 10 por ejemplo, y ya sabemos que debemos sumar la altura de ola a la total, de forma que un caso se convertiría en 6 m y el otro en 10,5.

…

[Keith11]

magistral...

ahora solo te falta tabular una relacion de diametros de cadena (8-10-12), con profundidades, con fuerza del viento y longitudes largadas en la condicion mas desfavorable, o sea la que llamas limite, ... y largando mas cadena que eso fondearemos mas tranquilos que un pancho

felicitaciones por el curro... tiene pinta de ser muy riguroso

[patxikiter]

el capitan al oficial

-Si estamos fondeados y arrecia el viento que hacemos?
*Largar mas cadena.
-Y si arreci amas??
*pues largar mas cadena.
-Y si vuelve a arreciar?
*Pues mas cadena capitan

-De donde saca usted tanta cadena?
*pues del mismo sitio que usted tanto viento

[pibronco]

Muy buena explicación.
Vaya curro, así da gusto.
Teniendo en cuenta que ante una duda técnica, si se puede y se sabe, mejor es hacer el cálculo teórico, que es la primera aproximación.
Los lobos de mar ya lo harán a ojo de buen cubero, pero el que pueda, quiera y tenga tiempo, mejor que calcule, y luego observe.
Por cierto, unas que te lo has ganado.

[mariner]

No sé cómo, pero se me había pasado por alto este post, que mas que tal, es todo un "Viaje al fondo del mar". Lo he leido encantado de principio a fin. Y, una vez más, tengo que hacer pública mi satisfacción por el nivel de esta Taberna y sus cofrades. Gracias MasBarco y a todos los que habeis aportado vuestro granito de arena.

Es increible lo que, en determinadas cabezas, puede provocar una pregunta tan tonta como "¿me interesa cambiar la cadena de 8mm por otra de 10mm?". Tan increible como la generosidad de hacer mil calculos y compartir sus conclusiones con el resto de los cofrades.

Así que, gracias de nuevo y tomaros unas que os las habéis ganado con creces
Mariner

[Mascocó]

COLAMBRE, gracias por rescatar el hilo de las profundidades, mi límite de buceo anda, andaba, por los cuatro metros/págs. así que yo ya no llegaba. Por cierto que tendré que darme prisa porque esto se hunde rápidamente y aquí no hay SM que valga, afortunadamente solo es un hilo.

Digo gracias porque tenía pensado retomar algunas cosas que había dejado un poco en el aire en algún post pasado, como lo de la influencia de un peso colgado en la línea de fondeo y también ver la magnitud de fuerzas verticales en el ancla una vez superada la catenaria límite, pero las matemáticas me parecían demasiado complicadas para abordar el tema aquí.

Sin embargo, una vez puestos, el planteamiento al menos, resulta relativamente sencillo, lo difícil resulta la resolución de la ecuación que se obtiene, de la que, como veremos, no se puede despejar la incógnita deseada. Sin embargo, utilizando la función Solver de Excel y creando una macro para utilizarla se pueden obtener los resultados. El procedimiento es un tanto tedioso en cualquier caso, pero al menos factible.

Esto es lo que trataré de desarrollar en los siguientes posts. Volveré a ser un tanto pesadito así que, el que se anime, que tenga paciencia conmigo. Presentaré primero la resolución general por si alguno encontrais un error en el planteamiento teórico.




PD. He cargado el programa que referenciaba COLAMBRE en su post, sin embargo, lo veo poco aplicable a nuestro caso ya que el peso unitario, en Kgs, no admite decimales, lo mismo que la tensión aplicada, en Tons, que tampoco.

[Mascocó]

El estudio completo de la línea de fondeo.

Voy a plantear la resolución de una línea de fondeo más complicada que lo que hemos visto hasta ahora, concretamente una dividida en dos trozos de diferente o igual peso unitario y colgando en su unión un cierto peso, y que además considere el caso en que la fuerza horizontal aplicada supera a la que forma la catenaria límite, es decir, cuando aparece fuerza vertical en el ancla.

Lo haré dividiendo el análisis en el de cada trozo de línea, que en este caso no tendrán que formar una catenaria completa sino dos arcos de catenaria, no presentaré un nuevo dibujo, pero creo que se entenderá si haceis referencia a los anteriores de la catenaria.

A cada uno de los trozos de línea le podré aplicar las siguientes ecuaciones de la catenaria:

siendo:

x es la distancia horizontal desde el origen de la catenaria completa al punto
y es la distancia vertical desde el origen de la catenaria completa al punto
FH la fuerza horizontal que forma la catenaria
FV(x) la fuerza vertical en el punto x
p el peso unitario por unidad de longitud

La ecuación general de la curva: y(x)= (FH/p).[cosh(p.x/FH)-1]

y su derivada: y’(x)= sinh(p.x/FH)

Esta última expresa la pendiente de la curva en el punto de abcisa x, que, como sabemos, coincide con la tangente del ángulo z(x) que forma la pendiente en el punto con la horizontal, es decir:

y’(x)= tg[z(x)]

como tg[z(x)]= FV(x)/FH

sinh(p.x/FH)= FV(x)/FH y, despejando x,

x= (FH/p).asinh[FV(x)/FH]

para un cierto tramo de catenaria, de valores de x x1 y x2 resulta:

y(x2)-y(x1)= (FH/p).[cosh(p.x2/FH) - cosh(p.x1/FH)]

donde:

x2= (FH/p).asinh[FV(x2)/FH]
x1= (FH/p).asinh[FV(x1)/FH]

si definimos:

at= y(x2)-y(x1)
X2= asinh[FV(x2)/FH]
X1= asinh[FV(x1)/FH]

nos queda:

at= (FH/p).[cosh(X2) - cosh(X1)]

donde:

at es la altura del tramo de catenaria estudiado
FV(x2) la fuerza vertical en su extremo superior
FV(x1) la fuerza vertical en su extremo inferior
FH la fuerza horizontal, la misma en todos los puntos (en nuestro caso es la que ejerce el viento sobre la embarcación)
p el peso por unidad de longitud

En nuestro caso estamos estudiando dos tramos de catenaria unidos que definimos como de alturas ar y ac, pesos unitarios pr y pc y longitudes Lr y Lc, luego:

Xr2= asinh[FV(xr2)/FH]
Xr1= asinh[FV(xr1)/FH]
ar= (FH/pr).[cosh(Xr2) - cosh(Xr1)]

Xc2= asinh[FV(xc2)/FH]
Xc1= asinh[FV(xc1)/FH]
ac= (FH/pr).[cosh(Xc2) - cosh(Xc1)]

Si nuestra altura total (ya sabemos, profundidad+altura roldana) es a:

a-ar-ac=0

Veamos ahora qué es lo que conocemos de todo esto. Para el primer tramo de la línea, desde la roldana, el de longitud Lr, tenemos, llamando M al peso colgado al final del tramo:

FV(xr2)= pr.Lr+M+pc.Lc+FVa
FV(xr1)= M+pc.Lc+FVa

Para el segundo tramo, el que llega hasta el ancla:

FV(xc2)= pc.Lc+FVa
FV(xc1)= FVa

FVa es la fuerza vertical en el ancla.
FHa= Fv= FH es la fuerza horizontal en el ancla.

Con esto obtenemos una expresión para a-ar-ac=0 en función de FHa y FVa, dando valores a una de estas dos incógnitas obtenemos, es decir, la función Solver obtiene, mediante iteraciones la otra.

[Mascocó]

Fuerzas verticales en ancla.

Este es el caso más sencillo, solo hay un tramo, el Lc, y tampoco hay peso colgado en la línea, las ecuaciones se reducen a:

FV(xc2)= pc.Lc+FVa
FV(xc1)= FVa

Xc2= asinh[(pc.Lc+FVa)/FHa]
Xc1= asinh[FVa/FHa]

a= ac= (FHa/pc).[cosh(Xc2) - cosh(Xc1)]

Dando valores a FHa según la velocidad del viento obtenemos FVa. Así, podemos obtener la siguiente gráfica:

fig.25

La gráfica está hecha para la fuerza de viento tomada para el Tin Tin (400 libras a 15 nudos), para una altura de 5 m y diversas relaciones de fondeo.

La fuerza horizontal en ancla se lee en la escala izquierda con la gráfica amarilla. La fuerza vertical en la escala de la derecha según la curva correspondiente a la longitud de cadena largada.

Se han representado las curvas para cadena de 8 y de 10 mm, alargando las longitudes de cadena de 8 mm (curvas de puntos) para obtener la misma fuerza de viento para la catenaria límite que para la cadena de 10 mm. Se puede observar las mejores prestaciones de la cadena de 8 mm, menor fuerza vertical generada en el ancla, debidas a su mayor longitud. Claro, que hemos tenido que largar más cadena y su carga de ruptura es menor, que como ya sabemos deberá tenerse en cuenta según el tamaño del barco.

Así, por ejemplo para 21 nudos de viento, la FHa será de 355 Kg, la FVa con 20 m de cadena de 10 mm, 69 Kg y con 25 m de cadena de 8mm, 55 Kg. Para estas longitudes, por debajo de 10 nudos de viento no se genera fuerza vertical.

Como se puede ver, la FVa crece rápidamente, aunque no en la misma medida que si la calculáramos simplemente según el ángulo de tiro que da la relación de fondeo, sobretodo al principio (a medida que aumenta FHa ambos resultados se aproximan), con lo que se ve la importancia de evitar la aparición de esta fuerza vertical largando más cadena, al final el resultado va a venir dado por el ancla misma y por como esté de agarrada al fondo, pero parece difícil esperar que un ancla de 20 o 30 Kg aguante una fuerza vertical de, pongamos, 60 u 80 Kg sin despegar del fondo.

Una gráfica más para alturas de 10 y 20 m:

fig.26

[Mascocó]

Línea de fondeo compuesta por cabo+cadena.

Ya habíamos estudiado este caso anteriormente, haciendo la aproximación de que la parte compuesta por cabo no formaba catenaria sino una línea recta y advertiendo que cometíamos un error, muy pequeño para longitudes grandes de cadena en relación al total, y mayor a medida que aumentaba la longitud de cabo. Este estudio, más completo, confirma esas previsiones, si comparais las gráficas que obtenemos vereis que el error anterior es casi despreciable para relaciones Lc/Lt mayores de 0,5.

En este caso hay dos tramos, sin peso entre medias, y calculamos para la catenaria límite, así que FVa=0:

FV(xr2)= pr.Lr+pc.Lc
FV(xr1)= FV(xc2)= pc.Lc
FV(xc1)= 0

pr, Lr y Pc, Lc son los pesos unitarios y longitudes respectivas de cabo y cadena.

Para una cierta longitud y altura de catenaria y variando la proporción de cadena sobre el total, podemos calcular cada FHa que provoca la catenaria límite y obtener su porcentaje respecto a la máxima, lo que nos permite dibujar la siguiente gráfica:

fig.27

Esta gráfica, valorada en FHa para a= 8 m, relación 10:1 en la escala izquierda, utiliza cadena de 10 mm y cabo de 16 mm al igual que en el anterior estudio, tiende al valor correcto para la línea de todo cabo que ya se comentó anteriormente, aunque la diferencia con la gráfica obtenida por el método simplificado es muy pequeña, del orden del 2,5% para Lc/Lt=0,4, y disminuyendo rápidamente hasta Lc/Lt=1.

Como ya he dicho, la gráfica está hecha para 8 m pero si variamos la profundidad y mantenemos la misma relación de fondeo la forma de la gráfica es exactamente la misma, es decir los valores FHa/FHa máx serán los mismos aunque, lógicamente, variarán los valores de FHa obtenidos.

Si variamos la relación de fondeo la curva también varía, pero muy ligeramente. Para observar esa variación he dibujado dos curvas para valores, un tanto extremos, de relaciones 3:1 y 10:1, como se ve, la diferencia entre las dos es casi nula, del orden del 2% máximo en el centro de la curva, evidentemente volverán de nuevo a variar los valores absolutos de las fuerzas.

Si variamos los diámetros de cadena y cabo empleados en la línea y mantenemos la relación de pesos unitarios de cadena y cabo pc/pr igual a la actual para cadena de 10 mm y cabo de 16 mm, las curvas resultan exactamente las mismas. Si esa relación de pesos varía, variarán también los porcentajes FHa/FHa máx. pero, de no ser muy exagerado el cambio, en poca medida y, lo que es más importante, las diferencias se centran en la parte baja de la curva.

Por tanto creo que podemos generalizar, para cualquier profundidad y relación de fondeo utilizadas y, dentro de unos límites razonables, también para cualquier combinación de cabo/cadena, la conclusión que sacamos en el primer análisis de la poca pérdida en eficiencia de la línea de fondeo que resulta al añadir cabo a la cadena, en lugar de todo cadena, mientras conservemos unas relaciones Lc/Lt altas, digamos por encima de 0,7, sobretodo comparando esa pérdida con el ahorro de peso en cadena obtenido.

[Mascocó]

Línea de cadena con peso. Incremento de FHa soportada.

Anteriormente hice algún comentario sobre la influencia de un peso colgado en un punto de la línea de fondeo. Básicamente llegaba a la conclusión de que para longitudes grandes de cadena la influencia del peso, frente a un peso mucho mayor de la cadena, iba a ser mínima. Concretamente decía algo así como que, en el mejor de los casos, la mejora iría pareja a la proporción entre el peso añadido repartido a lo largo de la cadena al peso unitario de la misma y que seguramente sería menor todavía. Bueno, veámoslo con un poco más de análisis.

Este caso es similar al anterior de cabo+cadena, es como si fueran dos tramos de línea de igual peso unitario con un peso M colgado en la unión entre ellos, de nuevo, FVa=0. Tendremos entonces:

FV(xr2)= pc.Lc+M
FV(xr1)= M+pc.(Lc–Lp)
FV(xc2)= pc.(Lc-Lp)
FV(xc1)= 0

Lp es la longitud de línea, desde la roldana, hasta el peso. Lc la total de cadena.

De nuevo, para cada longitud (Lc) y altura de catenaria, variando la posición del peso en la línea (Lp), podemos calcular cada FHa que hace FVa=0, en este caso, para lo que nos interesa, lo expresaremos como incremento en porcentaje respecto a la mínima, los resultados los representamos en la siguiente gráfica:

fig.28

Lo primero que podemos observar es que para longitudes cortas de línea la FHa necesaria para formar la catenaria límite aumenta grandemente, así, por ejemplo para a= 5m y Lc= 15m (relación 3:1), la FHa prácticamente se dobla para Lp/Lc=1. Ahora bien, Lp/Lc=1 significa que estamos poniendo el peso exactamente en el arganeo del ancla, el incremento de FHa obtenido es sencillamente el necesario para levantar ese peso, pero no hay contribución al efecto catenaria en sí, en cuanto baje un poco el viento el efecto del peso es nulo.

En el extremo contrario, Lp/Lc=0, tenemos el peso en la roldana, evidentemente su efecto es nulo y para eso mejor lo tendríamos sobre la quilla.

Por tanto se precisa de un compromiso, al menos a nivel de análisis, así que, aunque teóricamente cuanto más bajo esté el peso mejor, hay que tener en cuenta que cuando baje el viento el peso debe estar por encima del fondo para conservar su utilidad (y además para que no se enrede la línea si lo hemos largado con una). Para profundidades entre 5 y 10 m el peso debería estar aproximadamente al centro de la línea para quedar a una altura aproximada de 1 m sobre el fondo, para profundidades mayores podríamos bajar más el peso pero su altura sobre el fondo disminuye rápidamente a poco que baja el viento, más que nada por las normalmente altas longitudes de cadena asociadas y además hay que tener en cuenta que si lo hemos largado con una línea dejándolo deslizar a lo largo de la cadena manejar más de 40 ó 50 m de cabo comienza a ser complicado. Así pues parece razonable estimar una situación del peso a la mitad de la línea para el análisis, es decir Lp/Lc=0,5. Evidentemente, cuanto más larga sea la línea más atentos tendremos que estar a la situación del peso cuando disminuya el viento.

Los incrementos de fuerza así obtenidos para Lp/Lc=0,5 corresponden bastante aproximadamente a los calculados suponiendo el peso repartido uniformemente a lo largo de la catenaria (M/Lc/pc), concretamente son, respectivamente para las curvas del gráfico: 44,4% (40,4%), 22,2% (21,8%), 22,2% (20,4%), 11,1% (10,9%), 8,3% (8,0%) y 5,6% (5,5%) correspondiendo las cantidades entre paréntesis a las reales y las otras a la aproximación repartiendo el peso, así que se podría utilizar esta aproximación para el cálculo sobre el terreno, digo sobre el fondeo.

No es mi intención sacar muchas conclusiones de esto, cada uno sacará la suya propia desde luego, pero mi opinión vuelve a ser que utilizar este sistema de pesos colgados en la línea solo resulta interesante para longitudes de ésta muy cortas, cuando se hace necesario reducir el radio de borneo en fondeaderos muy atestados y cuando no se espera mucho viento y además podemos andar pendientes de la posición del peso, en otro caso, su utilidad frente al engorro de su manejo me parece muy limitada y vuelvo a preferir invertir parte de ese peso en el ancla misma y su coste en el diseño del ancla.

[Mascocó]

Línea de cadena con peso. Fuerzas verticales en ancla.

Por último presentaré una grafica comparativa de las fuerzas originadas en el ancla con y sin peso. Las ecuaciones asociadas ya las hemos visto con anterioridad.

fig.29

De nuevo, las curvas están calculadas para Fv= 400 libras a 15 nudos, para cadena de 10 mm y con relación de fondeo de 5:1 en todos los casos, presentando resultados para alturas totales de 5, 10 y 20 m, las líneas continuas corresponden a la línea sin peso y la discontinuas a la linea cargada con 15 Kg a la mitad de su longitud.

El beneficio del peso se muestra en retrasar la aparición de fuerza vertical (1,6 nudos más tarde para 5 m y 0,8 nudos para 20 m) y en disminuir ésta en unos 7 Kg más o menos linealmente.

[Mascocó]

Y con estas últimas intervenciones creo que ya termino, la verdad es que me he quedado a gusto, al menos creo que, dentro de mis posibilidades, al final le he dado un buen repaso al fondeo, al teórico quiero decir, con el otro me quedan todavía cosas pendientes, como que tengo una puntera que es una caca que tengo que reforzar y que el ángulo de tiro del molinete no es correcto y también tengo que corregirlo. Y también aprender a no perder más anclas.

Ahora aquí toca fondear, el hilo digo, y soltar mucha, mucha cadena por que me da que se va a ir al fondo, a profundidades abisales… rapidito, rapidito. Más que fondear creo que será dejarlo caer por su propio peso, sin grillete ni nada.

Salud.


PD. Realmente hubo un momento en que me obsesioné con la idea de ser la reencarnación de una bailaora que se llamaba “La Catenaria”.

[LORDRAKE]

Amigo MASBARCO hace tiempo que me quite el sombrero....
Tengo que leer esto con detenimiento....
Solo te pido una cosa, que comentes las conclusiones en palabras asequibles en cada supuesto.
Gracias


LORDRAKE

[Voras]

gran hilo...

Felicidades y gracias

[Mascocó]

Originalmente publicado por LORDRAKE

...
Solo te pido una cosa, que comentes las conclusiones en palabras asequibles en cada supuesto.
...

Sinceramente LORDRAKE, no lo acabo de pillar. No sé si te refieres a que haga una especie de resumen de lo que ha ido saliendo a lo largo del hilo o concretamente sobre mis últimos planteamientos, o a que soy demasiado críptico en mis conclusiones. Probablemente sea verdad que en mis últimos post haya dado por supuesto cosas que se han ido desarrollando a lo largo del hilo y que ya sean obvias para mi, que he metido muchas horas, pero no para cualquiera que no haya seguido el hilo a fondo. En cualquier caso, si te refieres es a alguna cuestión en particular tú dirás, pero, en fin, que no acabo de entender bien a lo que te refieres.

Saludos y gracias por seguir ahí. Lo mismo para los demás.

[Keith11]

MasBarco... no me funciona el excel...

a la que modifico una variable (las celdas en verde, supongo) la curva roja se me queda pegada en el eje de abcisas, y por mas que modifique las variables, ya nunca sale de esa posicion...

¿tienes idea de que puede estar pasando?

Saludos y

[mariner]

[quote=MasBarco;419770]

Ahora aquí toca fondear, el hilo digo, y soltar mucha, mucha cadena por que me da que se va a ir al fondo, a profundidades abisales… rapidito, rapidito. Más que fondear creo que será dejarlo caer por su propio peso, sin grillete ni nada.

Salud.


Pues mucho me temo que este hilo no toque fondo pues es mucho el interés que despierta cofarde MasBarco.

Visto según las pruebas que el metodo de 3 o 5 veces la profundidad no es quizá lo más adecuado, me pregunto si el anglosajón es mas efectivo.

Según tengo entendido, consiste en soltar SIEMPRE 12 metros más 2,5 veces la profundidad del lugar, entendiendo ésta como la altura existente desde la roda de la embarcación hasta el fondo en marea ALTA.

Lo cierto es que aplicando dicha formula, la cadena a largar difiere a veces considerablemente de lo que solemos hacer. Así por ejemplo:

Para 3 metros, en vez de 9 o 15 metros, largariamos 18,5
Para 5 metros, en vez de 15 o 25 metros, largariamos 24,5.
Para 10 metros,en vez de 30 o 50 metros, largariamos 37, y
Para 15 metros, en vez de 45 o 75 metros, serían 49,5

¿Cómo quedaría este método según "nuestros" calculos? Te lo digo porque yo la veo un poco escasa para fondear en profundidades importantes y por eso no la suelo aplicar.

Un saludo de nuevo y birras pàra todos
Mariner

[Mascocó]

Originalmente publicado por mariner

...
Visto según las pruebas que el metodo de 3 o 5 veces la profundidad no es quizá lo más adecuado, me pregunto si el anglosajón es mas efectivo.

Según tengo entendido, consiste en soltar SIEMPRE 12 metros más 2,5 veces la profundidad del lugar, entendiendo ésta como la altura existente desde la roda de la embarcación hasta el fondo en marea ALTA.

Lo cierto es que aplicando dicha formula, la cadena a largar difiere a veces considerablemente de lo que solemos hacer. Así por ejemplo:

Para 3 metros, en vez de 9 o 15 metros, largariamos 18,5
Para 5 metros, en vez de 15 o 25 metros, largariamos 24,5.
Para 10 metros,en vez de 30 o 50 metros, largariamos 37, y
Para 15 metros, en vez de 45 o 75 metros, serían 49,5

¿Cómo quedaría este método según "nuestros" calculos? Te lo digo porque yo la veo un poco escasa para fondear en profundidades importantes y por eso no la suelo aplicar.

Un saludo de nuevo y birras pàra todos
Mariner

Hola Mariner, creo que este método que indicas se basa en que, a medida que aumenta la profundidad, se necesita menor relación de fondeo para obtener los mismos resultados, cosa que ya hemos comentado aquí, mientras que el que solemos usar, más simple, el de 3 a 5 veces la profundidad, no considera esto. Es curioso que incluye el efecto de la marea, que en el Mediterráneo lo tenemos un tanto olvidado por ser básicamente mareas de presión, que me parece muy correcto si vas a permanecer en el fondeo un cierto tiempo, lo único, remarcar que la medida de profundidad debe ser la distancia vertical desde la roda, la roldana diría yo, hasta la horizontal desde el ancla, es decir la profundidad a que está fondeada el ancla+distancia roldana al agua+Incr.por marea, y, si me apuras +altura de ola.

En cuanto al método en sí pues seguramente adolece de los defectos de cualquier generalización, a mi en principio también me parecería que se queda corto a medida que aumenta la profundidad, pero en fin, luego está lo que importa, que es el viento que tenemos realmente, pero creo que todos sabemos que cuando soplan 20 ó 30 nudos no nos basta con una relación 3:1 por ejemplo, y que hay que largar más cadena. Creo que el método de curvas que hemos visto aquí es más exacto porque se adecúa al viento esperado pero claro, tienes que tenerlas.

En cualquier caso veamos la comparación con las curvas del Tin Tin (eslora 15m, manga 4 m) por ejemplo:

prof. 3m:
relac. 3:1, 9 m cad.10 viento en catenaria......... 5,7 nudos
relac. 5:1, 15 m cad.10 viento en catenaria........ 9,9 nudos
12+2.5x3, 18,5 m cad.10 viento en catenaria.... 12,4 nudos

prof. 5m:
relac. 3:1, 15 m cad.10 viento en catenaria...... 7,4 nudos
relac. 5:1, 25 m cad.10 viento en catenaria..... 12,8 nudos
12+2.5x5, 24,5 m cad.10 viento en catenaria... 12,6 nudos

prof. 10m:
relac. 3:1, 30 m cad.10 viento en catenaria.... 10,5 nudos
relac. 5:1, 50 m cad.10 viento en catenaria.... 18,2 nudos
12+2.5x5, 37 m cad.10 viento en catenaria..... 13,2 nudos

prof. 15m:
relac. 3:1, 45 m cad.10 viento en catenaria.... 12,8 nudos
relac. 5:1, 75 m cad.10 viento en catenaria.... 22,2 nudos
12+2.5x5, 49,5 m cad.10 viento en catenaria.. 14,3 nudos

Pues fíjate que lo que parecía escaso para mayor profundidad no lo es tanto, el método anglosajón por lo menos es bastante más equilibrado que el otro, varía entre 12,4/14,3 nudos frente a 5,7/12,8 en 3:1 y 9,9/22,2 para 5:1. Otra cosa es el límite de viento que aguanta, que tampoco está tan mal para un fondeo normalmente abrigado, pero ahí está la intervención del patrón.

Para un velero de 11m, 3,6m de manga, cadena de 8 mm daría:
prof. 5m, 24,5 m cad.8 ........ 11,0 nudos
prof. 10m, 37 m cad.8 ......... 11,6 nudos
prof. 15m, 49,5 m cad.8 ...... 12,5 nudos

No está mal.

Pero como método, método yo recomendaría... el mío. Es decir, descargaros la hoja de cálculo, meteis los datos de vuestro barco y la cadena y ya solo queda irse con el portátil al barco, meter los datos de profundidad y viento esperado y la hoja os dice cuánta cadena debeis soltar. No, en serio, siempre podeis imprimir algunas hojas con los graficos para las profundidades más utilizadas y tener esas hojas en el barco, así, sin regla ni lápiz, con el dedo mismo, podeis ver la cantidad de cadena a largar. Y luego, jeje, largais un poco más.

[Tucana]

Originalmente publicado por Mascocó

Hace un par de semanas, en el transcurso de unas prácticas, uno de nosotros planteó la siguiente cuestión:

¿Me interesa cambiar la cadena de 8 mm. por otra de 10 mm.?.

Pensando en lo que sabía de su barco, velero, algo más de 11 m. de eslora, manga contenida aunque desplazamiento también posiblemente más alto para lo que se estila ahora, mi primera respuesta fué en el sentido de que, si bien ganaría a la hora de fondear iba a perder prestaciones de navegación al aumentar mucho el peso de cadena en el pozo de anclas y que, no necesitándolo imperativamente por el tipo de barco, no le valdría la pena. Otra postura que surgió, en el sentido de que sí le interesaría, decía que siempre podría tener menos longitud de cadena de 10 mm, con lo que se compensarían los pesos y que necesitaría largar menos cadena a la hora de fondear, y también el compensar la menor longitud de cadena con más cabo.

Esto me hizo imaginarme la forma de la curva de una cadena más corta y más tensa y tirando hacia arriba del ancla, así que, recordando el estudio de la catenaria en la Escuela (años ha, muchos jeje) dije que la forma de la curva era siempre una catenaria que dependía de la longitud y no del peso de la cadena, con lo que una cadena más corta tendría necesariamente que tirar del ancla con un ángulo más desfavorable. Pero enseguida me dí cuenta que eso podía ser cierto pero que lo que también iba a hacer una cadena más pesada era acercar el barco al ancla, con lo que, al final, aún siendo más corta la cadena de 10, la curva podía ser la misma, o mejor.

Bueno, la cosa se quedó ahí, tampoco había mucho tiempo para insistir en la discusión. Pero yo me quedé con la mosca detrás de la oreja, por un lado porque no estaba completamente seguro de que lo que había dicho de que a igual longitud igual catenaria fuera exacto y por otro porque seguía con la duda de que se pudiera compensar el peso disminuyendo la longitud, más que nada por la idea de que siempre fondeamos con la relación cadena largada a profundidad.

Así que cuando volví a Madrid y tuve un rato, que al final ha sido un buen rato, me puse a investigar sobre las catenarias y los fondeos en internet y también en la Taberna. Bueno, decir que mi búsqueda de una fórmula aplicable para la catenaria fue bastante infructuosa, mucha ecuación diferencial, integraciones, ejes absolutos y canónicos etc… etc… pero nada que pudiera aplicar fácilmente en nuestro caso de fondeos, algo saqué en claro, al menos, y fué encontrar una demostración matemática de que no podía haber dos curvas catenarias diferentes con la misma longitud y la misma separación entre puntos de anclaje, con lo que efectivamente el peso no entra en la forma. También de paso me he enterado, que Galileo la confundía con la parábola, que hasta finales del XVII no se derivó su ecuación, que Miguel Angel tuvo que reforzar la base de la cúpula de la Capilla Sixtina con una cincha de hierro porque se agrietaba (no era catenaria) y que tuvimos que esperar hasta el siglo XIX para que arquitectos como Gaudí y su contemporáneo, y eclipsado por él, Luis Mancunill, utilizaran las propiedades del arco catenario… mientras que culturas del Islam lo utilizaron mucho antes y los sudaneses construían desde tiempos inmemoriales amplias habitaciones con forma de bóveda catenaria, de adobe, por la escasez de madera.

Pues no encontré nada útil hasta que se me ocurrió buscar catenary y rápidamente encontré esta página donde está todo lo que necesitaba:

http://mysite.du.edu/~jcalvert/math/catenary.htm


Bueno, como esto va a ser largo lo voy a desarrollar en unos cuantos post así que ponéos cómodos y algo de beber, que pago yo.

…

VHL. Very high level!!!