primeras líneas

[caribdis]

Originalmente publicado por Auskalo

Si tanta importancia le das al arranque manual puedes montar uno tipo sterling en casi cualquier motor.
Saludos
Auskalo.

Que es un arranque Sterling??

[Auskalo]

Son acumuladores de energia mecanicos, que luego accionan un motor de arranque. Hay varias marcas. Te permiten arrancar un motor sin necesitar electricidad.
Saludos
Auskalo

[Winder]

Aunque ya veo que se ha cambiado de tema, por si puede servir de algo

En cualquier cálculo de resistencia que hagamos, debemos aislar el elemento a estudiar (en este caso botavara), de todos los elementos que los sustentan ( en este caso: vela, cabos de escota, pajarín, pinzote y si consideramos necesario trapa) y sustituirlos por las reacciones de los mismos. En esta situación, el elemento a estudiar (botavara) deberá mantenerse estable, como si flotara en el aire. También podemos considerar el peso de la propia botavara.

Fig1 Si no tenemos en cuenta ni la trapa ni el peso de la propia botavara, consideramos la vela en crujía (ciñendo), y en esta situación cortamos la vela, las escotas, el pajarín y la botavara (esta última por una sección próxima al pinzote), sustituyéndoles por sus propias reacciones, la vela quedaría sustentada como se ve en la fig1. TV resultante de la vela, TE tensión de la escota de barlovento, TP resultante del pajarín, RH y RV reacciones horizontal y vertical en el pinzote.

Detalle-1 La vela ejerce una fuerza sobre la botavara TV que la podemos descomponer a su vez en dos fuerzas ortogonales, TB (en el plano de crujía) que tira de la botavara hacia arriba y hacia el pinzote, y TV1 (perpendicular al plano de crujía) que es la fuerza que hace girar la botavara hacia sotavento.

Detalle-2 Los 3 cabos de escota que van más a popa, ejercen sobre la botavara una fuerza (contenida en el plano que forman las dos escotas parte de popa) igual a 3 veces la tensión del cabo 3*TE, que la podemos descomponer en dos fuerzas ortogonales, TE2 que tira de la botavara hacia barlovento y es igual y de signo contrario a TV1 (contrarrestándose), y TE1 paralela al plano de crujía tirando de la botavara hacia abajo.

Detalle-3 El cabo de la escota que va más a proa, ejerce una fuerza sobre la botavara TE, que tira de esta hacia abajo y hacia proa.

Detalle-4 El pajarín ejerce una fuerza TP hacia proa

Detalle-5 El pinzote ejerce una fuerza sobra la botavara que descompuesta nos da una componente horizontal RH y una componente vertical RV

Fig-2 Una vez eliminados los cabos y la vela, podemos ver las fuerzas que actúan sobre la botavara manteniéndola en equilibrio y que están contenidas en el plano de crujía. Las fuerzas TE y TE1 se han trasladado a lo largo de sus propias direcciones hasta los puntos de fijación de las poleas en la botavara. Las fuerzas TV1 y TE2 no se han representando, porque son perpendiculares al plano de crujía y se equilibran entre ellas, si bien generan un par de rotación de la botavara = TV1*dmáx botavara.

Detalle-1 La fuerza TB tira de la botavara hacia arriba con TB*senD y hacia proa con TB*cosD

Detalle -2 La fuerza TE1 tira de la botavara hacia popa con TE1*cosB y hacia abajo con TE1*senB

Detalle-3 La fuerza TE tira de la botavara hacia proa con TE*cosA y hacia abajo con TE*senA.

Llegado a este punto la resolución de este problema es como ya expuse en mi intervención #1556 y que para los cálculos se puede utilizar la hoja excel que se encuentra en
https://drive.google.com/open?id=1W8...FaBnflzWfmaY5H
Donde se puede calcular RH y TB para distintas configuraciones, introduciendo diferentes valores de A, B, C, D, d1, d2, d3, TE, TP.

[Winder]

Una corrección, el pajarín no transmite ningún esfuerzo horizontal al pinzote.

Si el sistema de desmultiplicación va dentro de la propia botavara como es mi caso, lo que hace es aguantar la componente "TB" de la vela y someter a la botavara a un esfuerzo de compresión sin afectar al pinzote.

Si el pajarín sale por una polea del extremo de proa de la botavara y de hay a la base del palo y al piano, los esfuerzos horizontales se aguantarían en las dos poleas proa y popa de la botavara, sometiendo en esta un exfuezo de compresión y sin efecto sobre el pinzote. También se produciría un esfuerzo hacia abajo en el pinzote, igual a la tensión del pajarín. En este caso la tensión del pajarín también aguanta la componente "TB" de la vela.


Para tener en cuenta lo dicho he modificado la hoja de cálculo y he borrado la anterior. La modificada se encuentra en esta dirección
https://drive.google.com/open?id=1q4...B3-T8aSlTkj-6Y

[caribdis]

Originalmente publicado por Winder

Una corrección, el pajarín no transmite ningún esfuerzo horizontal al pinzote.

Si el sistema de desmultiplicación va dentro de la propia botavara como es mi caso, lo que hace es aguantar la componente "TB" de la vela y someter a la botavara a un esfuerzo de compresión sin afectar al pinzote.

Si el pajarín sale por una polea del extremo de proa de la botavara y de hay a la base del palo y al piano, los esfuerzos horizontales se aguantarían en las dos poleas proa y popa de la botavara, sometiendo en esta un exfuezo de compresión y sin efecto sobre el pinzote. También se produciría un esfuerzo hacia abajo en el pinzote, igual a la tensión del pajarín. En este caso la tensión del pajarín también aguanta la componente "TB" de la vela.


Para tener en cuenta lo dicho he modificado la hoja de cálculo y he borrado la anterior. La modificada se encuentra en esta dirección
https://drive.google.com/open?id=1q4...B3-T8aSlTkj-6Y

No he cambiado de tema, digamos que es obligatorio tratar varias cosas al mismo tiempo..

Si el pujamen fuera fijo directamente a la popa de la botavara habría que considerar la componente horizontal de esa fuerza, que se transmitiría como compresión al pinzote.

Si reenviamos pajarín hasta la proa de la botavara y lo mordemos allí, con las típicas mordazas en la propia parte inferior de la botavara, la compresión de la botavara sería doble, como habíamos visto que pasaba con las drizas, y la compresión en el pinzote también, es el mismo caso pero en horizontal.

Si en la proa de la botavara ponemos una polea y bajamos el tiro hasta la base del palo, tenemos una componente en la polea de popa entre la dirección de tiro del pujamen hacia el centro geométrico de la vela y la dirección de la botavara; y otra componente en la polea de proa entre la dirección de la botavara y la vertical hasta el reenvío de la base del palo.

Las tensiones son iguales en cualquier punto del cabo pero los ángulos no, y seguirá habiendo compresión en el pinzote, la que corresponda según los ángulos.

Un saludo

[iperkeno]

Al descender al detalle e intentar utilizar métodos de elementos finitos, no hay que perder de vista que los esfuerzos mayores son producidos por el viento y por las inercias... tanto que muchos de los otros, cuando se da el caso, pasan a ser despreciables o a multiplicarse, según los casos.

[Winder]

Tienes razón en lo que dices y yo creo que también la tengo en lo que dije en mi última intervención, me explico:

Si nos fijamos en el esquema que puse en mi intervención #1576 y concretamente en el detalle1 de la figura1, podemos concluir que de las dos componentes ortogonales en que se descompone la fuerza TV (resultante de todas las fuerzas de la vela sobre el puño de escota), la componente TV1 (perpendicular a la botavara)se aplicará en el patín de la vela, intentando abrir la vela hacia sotavento, mientras que la componente TB (contenida en el plano de crujía) se aplica en el pajarín (chicote que se fija en la vela) en la misma dirección que este sale de la polea de popa. Por esto último digo que la tensión del pajarín TP = TB.

Si ahora vamos al detalle2 de la figura1 intervención #1576, podemos ver que TB se descompone a su vez en dos componentes ortogonales, la componente horizontal igual a TB*cosD que somete al pinzote a un esfuerzo en dirección popa-proa y que se mantiene en todos los cálculos que he hecho. Es esta a la que te refieres cuando dices “Las tensiones son iguales en cualquier punto del cabo pero los ángulos no, y seguirá habiendo compresión en el pinzote, la que corresponda según los ángulos”.

Por otra parte, si cortamos el pajarín en un punto intermedio entre la polea de popa y proa, podríamos sustituir por dos fuerzas iguales de valor TP (tensión del pajarín) y de sentido contrario, una en sentido proa-popa y la otra en sentido popa-proa. Estas dos fuerzas no darían ninguna resultante sobre el pinzote, ya que son iguales y opuestas. La de sentido popa-proa (comprimiendo el pinzote) es la que he representado en la figura2 intervención #1576, pero como no he representado la de proa-popa, no quedaba compensada y por lo tanto el pinzote quedaba sometido a un esfuerzo TP (error), que es lo que he tenido que corregir.

[hibrido]

Originalmente publicado por iperkeno

Al descender al detalle e intentar utilizar métodos de elementos finitos, no hay que perder de vista que los esfuerzos mayores son producidos por el viento y por las inercias... tanto que muchos de los otros, cuando se da el caso, pasan a ser despreciables o a multiplicarse, según los casos.

Más razón que un santo
solo añadir que las velas son láminas y todos los esfuerzos están contenidos en su plano tangente en cada punto.
sobre las inercias, los esfuerzos debidos a las aceleraciones de cabeceo y balance pueden ser enormes.

[caribdis]

Originalmente publicado por Auskalo

Son acumuladores de energia mecanicos, que luego accionan un motor de arranque. Hay varias marcas. Te permiten arrancar un motor sin necesitar electricidad.
Saludos
Auskalo

He encontrado uno, Kineteco, tiene buena pinta, pero esto casi sería para desmontar el motor de arranque electrico y montar este en caso de quedarte sin batería, no?, y un motor de inyección indirecta como el Yanmar 3YM30AE siempre necesitaría carga..eso creo...



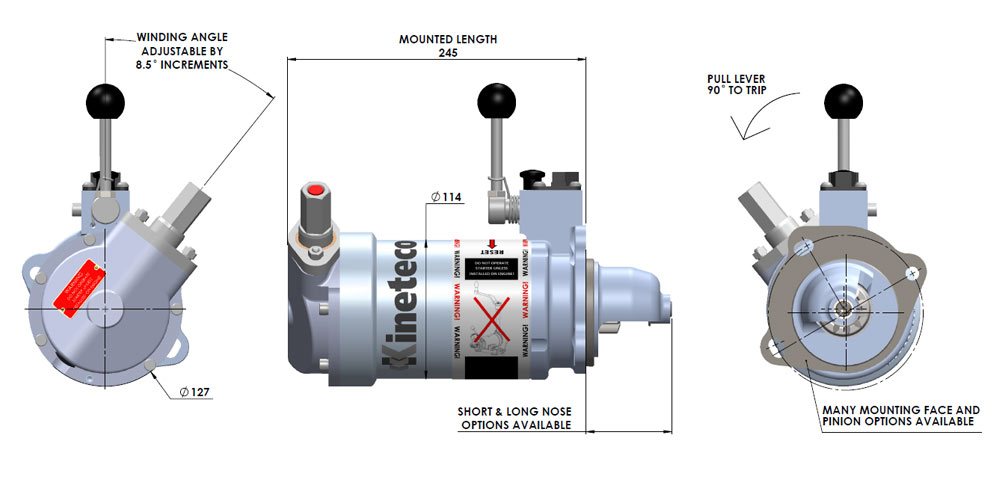http://www.springstarter.com/



Imagino que la opción de Bukh de arranque de muelle debe ser así, con dos motores en el volante de inercia, el eléctrico y el de muelle..