Qué es el seno?

[El Boquerón]

Después de leer en varias fuentes, no acabo de entender ´qué es el seno,coseno...Se que:

En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la Hipotenusa


El seno de un ángulo????????? parece porno
qué es ,qué mide...?
gracias cófrades.Anda que no me queda camino...!

[Capitán Trucho]

Esto es de lo más sencillo que he encontrado.

http://www.pvivov.net/matematicasbas...triabasica.pdf


Aquí hay más definiciones...

http://es.wikipedia.org/wiki/Trigono...om.C3.A9tricas

... y si tienes alguna duda concreta, pregunta que para eso está La Taberna.

[El Boquerón]

Gracias Capitán trucho. La duda concreta es que no se qué significa seno. La fórmula la conozco y dónde se aplica, también. Pero el valor del seno, qué mide ?

[jiauka]

El que está a babor o estribor del coseno, a veces hay alguna hipenetusa que los une.

[Capitán Trucho]

Originalmente publicado por El Boquerón

Gracias Capitán trucho. La duda concreta es que no se qué significa seno. La fórmula la conozco y dónde se aplica, también. Pero el valor del seno, qué mide ?

El seno de un ángulo varía de +1 a -1 y es una proporción (resultado de la división del cateto opuesto por la hipotenusa). Se usa para resolver triángulos del mismo modo que el coseno o la tangente.
Intenta hacer el ejercicio que te proponen que es un tema náutico...

http://www.juntadeandalucia.es/averr...gonometria.htm

Saludos.

[Capitán Trucho]

En este caso el seno del ángulo de observación es la altura de la torre dividido por lo que llaman "línea de visión".

seno del ángulo de elevación = altura de la torre / línea de visión. Si la altura de la torre es conocida, el ángulo lo has medido y calculado su seno (calculadora) puedes conocer a que distancia se encuentra el objetivo. Puede servir para que la foto no salga borrosa (modo políticamente correcto "on") aunque normalmente se usa en artillería (modo políticamente correcto "off")

Buenas tardes Sr. Boquerón,

Hombre, francamente, me ha sorprendido, y mucho, su pregunta a estas alturas, a su edad. Pero hace bien preguntando si no domina una cuestión tan importanter como el concepto de seno. Mire usted, había puesto una foto de un seno pero el servidor de Imageshack me la ha borrado porque dice que viola los términos del servicio... Virgen santa a lo que estamos llegando, ya no se puede poner un seno porque se viola no sé qué. En fin, la explicación no quedará igual de completa en mi opinión, pero vamos allá:

Mire, coja usted un ángulo cualquiera, como el ángulo alfa que le represento mediante las dos rectas azules que se cortan de la figura siguiente:



Si usted se fija, dado el valor del ángulo lo único que usted sabe es cómo de "abiertas" están las dos rectas (cuanto mayor sea el ángulo menos paralelas son, más abiertas están). Esa idea está muy bien, pero en matemáticas hay que poder cuantificar las cosas, hay que poder medirlas con precisión. Y para eso definimos una serie de NUMEROS que asignamos a cada ángulo. Para definir esos número lo que ha de hacer usted es trazar una recta perpendicular a una de las dos que definen el ángulo (la recta negra por ejemplo). Una vez hecho puede usted ahora medir dos DISTANCIAS (es decir, se miden con una regla, en centímetros, metros, millas náuticas, etc). Esas distancias son y_1, h_1. El seno del ángulo, escrito sen(alfa) ó sin(alfa), se DEFINE como el NUMERO que resulta de dividir y_1 / h_1. Si se fija usted se dará cuenta inmediatamente que lo que está haciendo de esta forma es, precisamente, medir cómo de abiertas están las dos rectas que definen el ángulo (o, en otras palabras, como de grande es el ángulo en sí): cuanto mayor sea alfa (cuanto más abiertas estén las rectas), mayorserá y_1 y, por tanto, mayorserá el cociente y_1 / h_1, o sea, mayor será el seno del ángulo.
¿Por qué le he dibujado las otras rectas, verde y roja, en el la figura anterior? Pues para hacerle ver a usted que el seno del ángulo no es más que otra manera de expresar la semejanza de triángulos: si usted divide y_2 /h_2 o divide y_3 / h_3 obtendrá EL MISMO resultado, sen(alfa). ¿Por qué? Porque sen(alfa), tal y como se define, no es más que la constante de proporcionalidad entre el cateto opuesto y la hipotenusa del triángulo rectángulo que ha quedado dibujado al dibujar la recta negra vertical. Es decir, es el número por el que hay que multiplicar la hipotenusa para obtener el cateto opuesto al ángulo en cuestión (por eso es menor que 1, porque el cateto es siempre menor que la hipotenusa). Pero si ahora se fija usted en el triangulo que queda dibujado con la línea vede, esa constante de proporcionalidad es NECESARIAMENTE la misma porque ambos triángulos son semejantes (esto es una manera de expresar el teorema de Tales de las matemáticas elementales), y lo mismo ocurre con el triángulo rojo porque también es semejante al negro y al verde.
Así que, resumiendo, el seno de un ángulo no es más que la proporción entre esos dos lados del triángulo rectángulo (el cateto opuesto al ángulo y la hipotenusa). ¿Por qué lo llamamos seno? Pues supongo que para jo..er. No hay ninguna razón en particular, son motivos históricos, de la época de los griegos que inventaron estas cosas...
Y si en lugar de utilizar los catetos que he llamado "y" en la figura de arriba utilizamos los catetos "x" (los que están al lado del ángulo y que no puesto en la figura para no complicarla) pues obtenemos la razón de proporcionalidad que llamamos coseno de alfa (escrito cos(alfa)). Y si hacemos la proporción entre el cateto opuesto y el contiguo puies obtenemos lo que llamamos tangente de alfa (tan(alfa)). No hay ningún otro misterio detrás de estos números.

En la práctica, para calcular el seno de un ángulo procederíamos entonces a dibujar ese ángulo con un transportador. Después trazamos una recta perpendicular a uno de los dos lados del ángulo en cuestión. Habremos dibujado así un triángulo rectángulo. Ahora medimos, en centímetros, con una regla la longitud de los tres lados (la hipotenusa y los dos catetos). Dividimos la longitud del cateto opuesto entre la longitud de la hipotenusa y obtenemos así un número (que NO tiene unidades porque es el cociente de dos magnitudes cada una de las cuales tiene la misma unidad) que es el seno del ángulo... Naturalmente, como nos hemos amariconado, en la práctica ya no lo hacemos así (y por eso se nos olvidan los conceptos). Ahora utilizamos una calculadora científica (nunca he sabido porqué la llaman científica). Apretamos una tecla y el chinito que vive dentro hace el dibujo, mide con la regla y hace la división por nosotros dándonos directamente el resultado final, todo con asombrosa rapidez. Estos chinos son la os..ia, se comerán el mundo.

Saludos,
Tropelio

[wiper]

Originalmente publicado por El Boquerón

Gracias Capitán trucho. La duda concreta es que no se qué significa seno. La fórmula la conozco y dónde se aplica, también. Pero el valor del seno, qué mide ?

Igual no te ayudo nada o igual te resuelvo el problema. La hipotenusa del triángulo que queda dentro de esa circunferencia es exactamente su radio.
Si consideramos el radio igual a uno o dicho de la misma forma a la unidad, sea esta unidad metros, kilómetros, millas náuticas, cables, brazas, pies castellanos o chinos o cualquier otra que pueda ser así representada, resulta que el seno es exactamente igual al cateto que queda representado verticalmente. El coseno, por la misma de tres, es el cateto que queda representado en la figura horizontalmente.
Si dibujas un ángulo Xº y mides con una regla esos catetos, veras que coinciden exactamente, con los valores de seno y coseno para ese ángulo.
La unidad será el radio y por tanto el seno y coseno serán de un valor inferior a él salvo en dos situaciones. La primera cuando el ángulo es 0º el seno es =0 y y el coseno= 1, es decir igual al radio. El segundo caso cuando el ángulo es 90º el seno es = 1 e igual al radio y coseno =0.
El problema es que la precisión que puedas conseguir midiendo con la regla es muy poca pero sirve para tener una imagen del asunto.

PD gracias Tropelio por tu esfuerzo, ahora me voy a tener que comprar esa nueva edición para estar al día, leches .

Edito y me explayo un poco más que luego te vendra bien: el coseno de 90º menos un ángulo Xº ( ángulo complementario de X) , es igual al seno de Xº, puedes dibujarlo y comprobarlo.
Todo esto considerando el radio como la unidad o igual a 1
Ya sabes que mis herramientas de dibujo son una merde pero ya nos entendemos.



Vuelvo a editar y lo remato. Fijándonos en el dibujo sabemos que el radio es la unidad y que coincide con la hipotenusa, tambien sabemos que el seno y el coseno son inferiores a ella o iguales. Prolongando las lineas, Si por ejemplo tenemos la hipotenusa de un triángulo que mide 10 unidades y un ángulo de 30º ¿Cuanto medira el cateto opuesto? En castellano raso, de pueblo y sin quitarme la boina, El seno "mide" lo que medira el cateto opuesto para cada una de las unidades que mida la hipotenusa en un triángulo rectángulo y un ángulo dado. chis pun. preguntabas lo que media y creo que esto responde.
Con esta pregunta creo que queda todo explicado.
Ma costao pero luego viene que si tanto de copa y tal y tal, que ya son números complejos.

Originalmente publicado por wiper

PD gracias Tropelio por tu esfuerzo, ahora me voy a tener que comprar esa nueva edición para estar al día, leches .

Hola wiper,

No es necesario comprar la nueva edición (cuando salga si algún día lo hace). El nuevo capítulo está disponible en mi web, en la página del libro, de manera gratuita para todo aquél que quiera leerlo o descargarlo (está en formato pdf). Pero, en cualquier caso, siempre te agradeceré la compra de la nueva edición, claro, tengo que pagar mi Swan 46 que encargué a cuenta de mis derechos de autor... Así que pondré una lista de las librerías en las que está disponible, como se estila en este foro

Saludos,
Tropelio

[wiper]

Hablando de senos, Les Luthiers. Carta de amor de Johan Sebastian Mastropiero a la Condesa de Shaarchat con la que mantuvo un fogoso romance:

"Querida Condesa, nuestro amor se rige por el Teorema Thales, cuando nuestros cuerpos se encuentran horizontales y paralelos, las transversales del amor nos atraviesan y nuestros segmentos son hermosamente proporcionales."

Fantástica analogía.

[Haize Alde]

Originalmente publicado por El Boquerón

Después de leer en varias fuentes, no acabo de entender ´qué es el seno,coseno...Se que:

En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la Hipotenusa

.

¿Y qué mas quieres? Es un valor adimensional.
Las operaciones con ángulos sirven para muy poco, sin embargo, con sus razones trigonométricas tienen utilidades infinitas.
Si no te lo crees te doy el teléfono de Pitágoras aunque no se si se pone.

[Haize Alde]

Originalmente publicado por El Boquerón

Después de leer en varias fuentes, no acabo de entender ´qué es el seno,coseno...Se que:

En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la Hipotenusa

La mejor explicación y la única la has puesto tú. El resto, adornar la burra.

[goro]

Qué es el seno?... y tú me lo preguntas?... el seno eres tú!



Fuera coñas!. El seno es una razón entre dos magnitudes mesurables (en nuestro caso, rumbo y distancia). Está en el mismo saco que el número pi, la razón aurea,....

Originalmente publicado por goro

Qué es el seno?... y tú me lo preguntas?... el seno eres tú!



Fuera coñas!. El seno es una razón entre dos magnitudes mesurables (en nuestro caso, rumbo y distancia). Está en el mismo saco que el número pi, la razón aurea,....

No. El rumbo es un ángulo mientras que la distancia es eso, una distancia. El seno NO ES la razón entre estas dos cosas.
Saludos,
Tropelio

[Bou Fort]

Buenassss, cajarillos al poder !

Pues no señor goro! rumbo y distancia nos dan un segmento orientado, y eso puede ser la representación de un vector, (I love vectors!).
Algún día abriré un hilo respecto a los vectores en náutica

Pero el seno.... el seno es otra cosa, es una razón goniométrica (una característica de un ángulo) como muy bien han explicado en este mismo hilo ilustres cofrades.

Saludos

F. Bou Fort

[Juanitu]

Esta claro. Si dejas que cada uno te cuente su película vas a acabar con un lío. Tropelio te pondrá al día de trigonometría. Una buena colección de cachondos mentales pondrán fotos de tetas (¡anda, ya las han puesto!).

Pues mira: los senos son unas cavidades que tenemos en los huesos alrededor de la nariz (paranasales) y la frente (frontales) rodeando la vía respiratoria nasal. Tienen mucha importancia en muchos aspectos, pero en esta Taberna nos afecta sobre todo a los buceadores, ya que forman parte del juego de compensación de presiones. Por eso no debe bucearse con ellos inflamados (sinusitis), obturados por moco (costipados), o encharcados (cuando se nos ha "llenado" la nariz de agua).




Pd. Espero aportaciones de los expertos en radio sobre ondas "senoidales" y tal...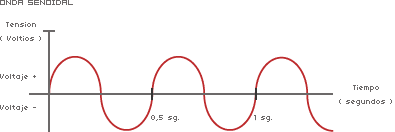


Pd: También sería interesante lo del "seno" de la ola... oceanógrafos.

[Capitán Trucho]

Originalmente publicado por Juanitu

Esta claro. Si dejas que cada uno te cuente su película vas a acabar con un lío. Tropelio te pondrá al día de trigonometría. Una buena colección de cachondos mentales pondrán fotos de tetas (¡anda, ya las han puesto!).

Pues mira: los senos son unas cavidades que tenemos en los huesos alrededor de la nariz (paranasales) y la frente (frontales) rodeando la vía respiratoria nasal. Tienen mucha importancia en muchos aspectos, pero en esta Taberna nos afecta sobre todo a los buceadores, ya que forman parte del juego de compensación de presiones. Por eso no debe bucearse con ellos inflamados (sinusitis), obturados por moco (costipados), o encharcados (cuando se nos ha "llenado" la nariz de agua).




Pd. Espero aportaciones de los expertos en radio sobre ondas "senoidales" y tal...


Pd: También sería interesante lo del "seno" de la ola... oceanógrafos.

¡Ahora por fin me he enterado!
Gracias Juanitu.

[kikot]

Un intento más de simplificación:
Cuando el círculo es de radio unidad (c=1) el seno es igual a a.


Saludos.

[Juanitu]

¡Como se nos ha podido olvidar EL SENO MATERNO!

[bogavante]

Mira que es fácil y como se enrollan:

el seno, el coseno, la tangente, ... no son si la razón (la división) de un lado de un triángulo rectangulo por otro. Es decir, por ejemplo, el seno es la proporción entre el cateto opuesto y la hipotenusa, de tal modo que si es igual a 0,5 quiere decir que el cateto mide la mitad de hipotenusa. Si la tangente es igual a uno, quiere decir que los dos catetos son iguales y así. Es decir son proporciones entre lados.


Un saludo y unas birras a mi nombre

[Tranes]

No era esto un foro nautico????

SENO: Se trata del arco o curvatura que forma el cabo entre los extremos que lo sujetan, bien cuando trabaja o bien cuando se manipula con él.


http://www.masmar.net/esl/N%C3%A1uti...,-Boza-y-Firme

[Capitán Trucho]

Voy a intentar explicarlo de forma sencilla que, después de las muy doctas enseñanzas de ilustres maestros, solo puede ser fruto de la osadía del ignorante.
Gráficamente resuelves un triángulo si te dan dos lados y el ángulo que forman. Dibujas uno de los lados con la longitud que te han dado. En una punta trazas el ángulo que también te dan. Sobre esta recta tomas la medida, que también te dan, y unes los extremos de los dos lados.
Matemáticamente tienes la dificultad de que los lados te los dan en unidades de longitud y el ángulo en grados sexagesimales, centesimales o en radianes. Este ángulo tienes que transformarlo en algo que se pueda multiplicar o dividir con las unidades de longitud. De ahí nacieron las funciones trigonométricas.
Saludos.

[wiper]

Boquerón, he editado el post nº 23 y creo que con lo que he añadido al final ya está claro para tener una imagen del tema.

[El Boquerón]

Originalmente publicado por wiper

Boquerón, he editado el post nº 23 y creo que con lo que he añadido al final ya está claro para tener una imagen del tema.

Saludos Wiper, te refieres a la hermosura de los segmentos ?