Navegación astronómica sin situación de estima

[Mascocó]

Para analizar la cuestión de la no convergencia presento los resultados para otros dos conjuntos de observaciones:


Observación de Alphecca y Capella:





Convergiendo a So1 (la supuesta real):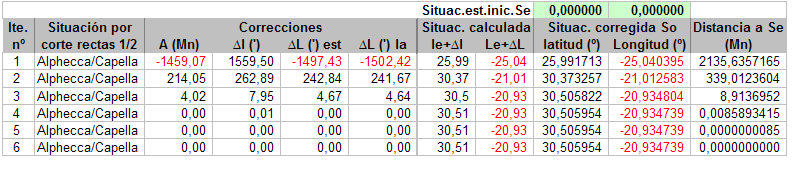





… y convergiendo a So2: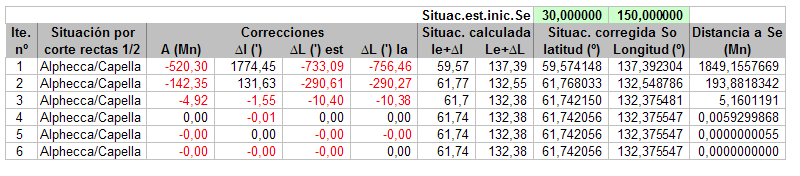







Observación de Mimosa y Denébola:






Convergiendo a So1 (la supuesta real):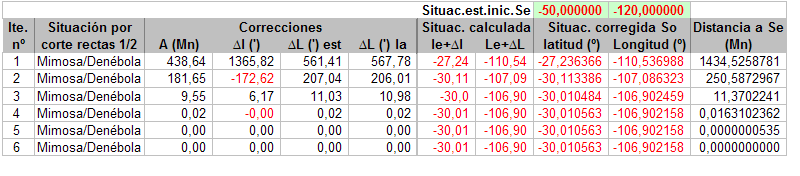





… y convergiendo a So2: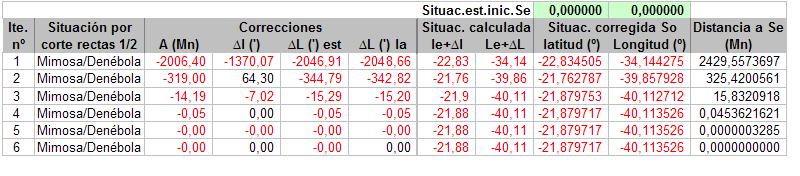






Para estos dos últimos conjuntos de observaciones no he encontrado Se iniciales para las que no haya convergencia, pero, no sé si curiosamente o no, volviendo al ejemplo de la observación que puso Tropelio, ahí si que se encuentran muchos puntos de Se para los que no se produce la convergencia, por ejemplo: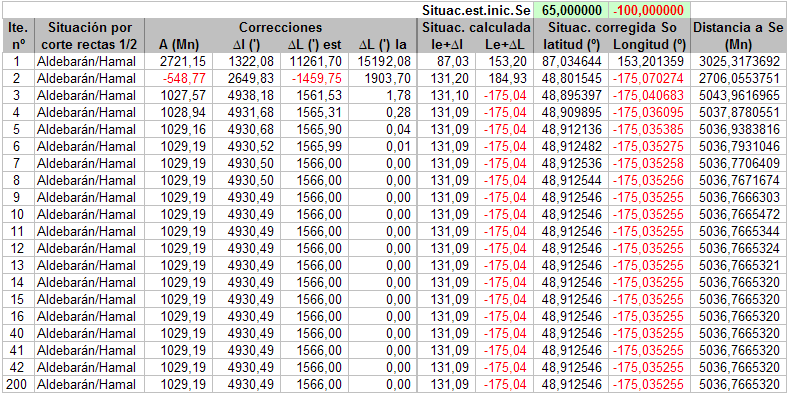




Como veis, aquí está probado con 200 iteraciones, pero para el caso es lo mismo probar con 1.000, se llega a una determinada situación que ya no converge más pero la distancia So/Se es sumamente grande.

Aunque, vuelvo a imaginarme, que casi seguro esto se debe a la aproximación de círculos a rectas, el caso es que estas situaciones de no convergencia no se encuentran en las otras observaciones que he probado, al menos para las situaciones que, manualmente, he ido probando, lo que me ha llevado enfocar el análisis de otra manera.




Sigo en otro post.

[Mascocó]

Dado lo tedioso de probar las situaciones iniciales una a una, he formado una nueva hoja de cálculo, con base la anterior, para permitir la generación automática de un mapa de convergencia.

Para el ejemplo de Tropelio los resultados son los siguientes: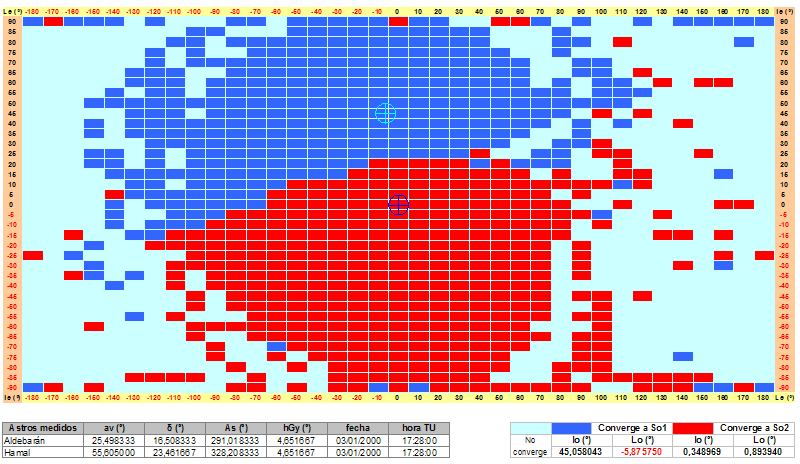



Las cuadrículas en azul indican la convergencia hacia el punto So1 (en principio nuestra situación real), las que están en rojo las de convergencia a So2, y el fondo azul claro las de no convergencia.

Evidentemente los cálculos no están realizados para cada punto de partida de Se, si no, en este caso, con intervalos de 5º en latitud y de 10º en longitud, para los puntos centrales de cada cuadro. Es decir, por ejemplo, el recuadro rojo que indica convergencia a So2 entre le=+/-2,5º,Le=+/-5º tiene un solo cálculo para le=0º,Le=0º.

Como se puede ver, el mapa de la observación Aldebarán/Hamal presenta amplias zonas de no convergencia. Los mapas están realizados con 20 iteraciones para cada punto de análisis, habrá alguno de los puntos que no convergen que lo harán con más iteraciones, como el ejemplo que puse para le=30ºN,Le=150ºE, que converge a partir de la iteración 25 y que en el mapa se presenta como no convergente, pero por lo que he podido ver, su número no es significativo en el mapa general.

Si ampliáramos la definición, por ejemplo para incrementos de 1º en latitud y 2º en longitud, obtenemos, para el intervalo le=20-35ºN,Le=040-070ºE: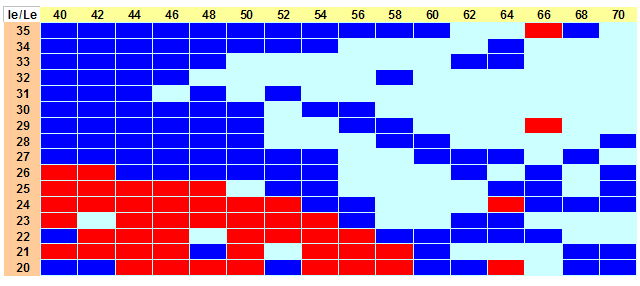



que, como se ve, no aporta nada nuevo.




Sigo en otro post.

[Mascocó]

Será casualidad, o no, pero las zonas de no convergencia no aparecen en las otras dos observaciones que he analizado.

Ni con Alphecca/Capella: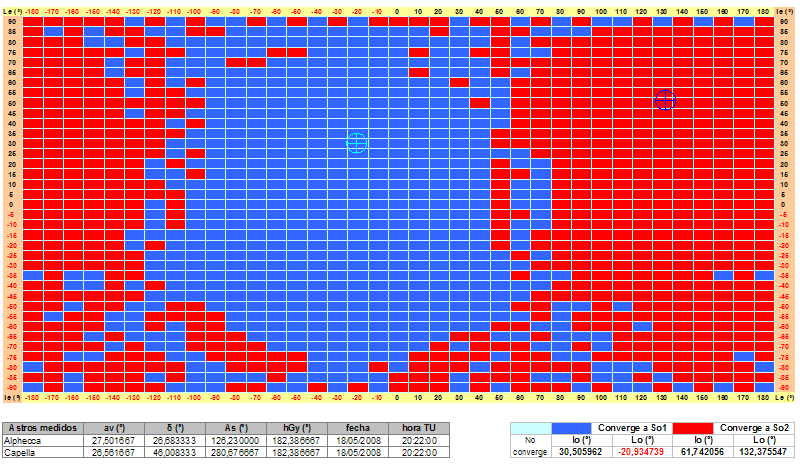




Ni con Mimosa/Denébola: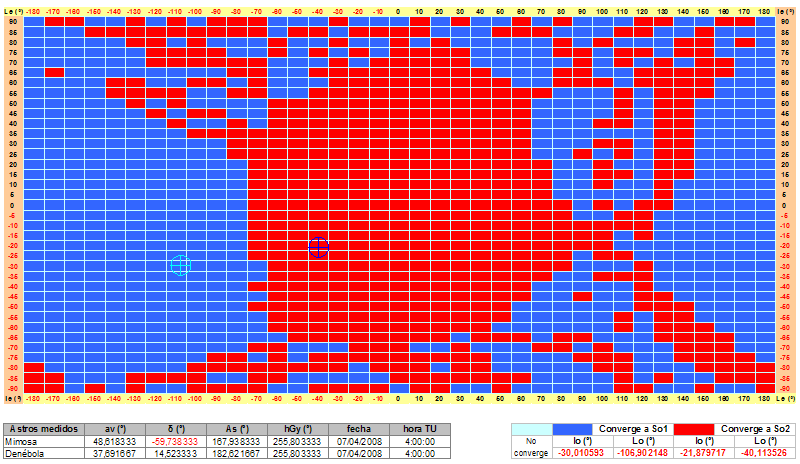




Como se ve, no aparecen zonas no convergentes. Aunque ampliemos la definición del análisis, no se obtienen puntos de no convergencia, incluso, como en el siguiente ejemplo de ampliación del análisis para Mimosa/Denébola, para una zona muy alejada de los puntos de convergencia y además de transición entre So1 y So2, y con intervalos de 0,5º de latitud y 1º de longitud: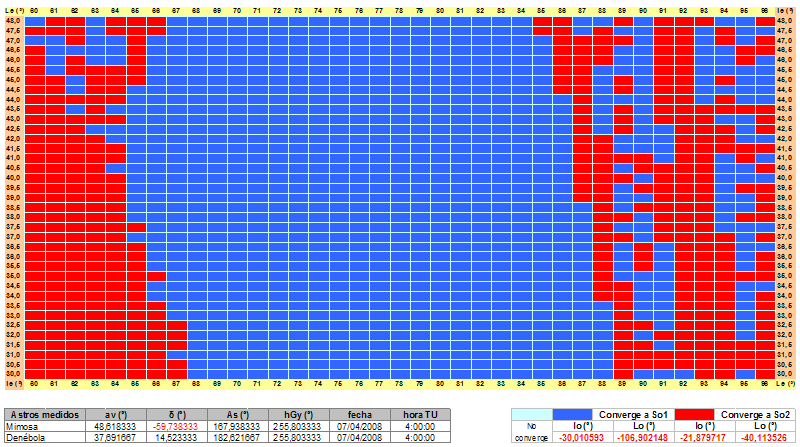




Realmente no sabría explicar esta diferencia con el ejemplo de Aldebarán/Hamal que puso Tropelio y que tiene tan amplias zonas de no convergencia, será quizás cuestión de los datos astronómicos de partida. Yo en principio pensaría que todas las Se de partida deberían converger, pero a ver si alguien lo puede explicar. Claro, que los ejemplos que convergen son de examen de la DGMM, ¿será eso?, je, je.

En todo caso, por supuesto que esto no invalida el método de iteración, partiendo de una situación con un mínimo de aproximación generalmente solo se necesitan tres o cuatro iteraciones para un resultado muy correcto. Como creo haberle leído a Tropelio basta con, sin conocer la situación de estima, escogerla con un poco de cabeza.




Y ya, termino en el siguiente post.

[Mascocó]

Y ya está, me ha salido un buen rollo, quizás para poca cosa podrá pensar alguno, hasta yo mismo, pero tenía curiosidad con esta historia de cálculos sin posición de estima.

Para el que quiera experimentar con las iteraciones sucesivas, al final del post, en Archivos adjuntos podeis descargar el que he utilizado en estos cálculos.


Como ya dije, el fichero es una hoja de cálculo en Excel. Para reducir el tamaño al mínimo se presenta con sólo 10 iteraciones, pero se puede ampliar con facilidad a las que se quiera.

Por supuesto se agradecerán las correcciones a cualquier error que podais encontrar, así como los comentarios sobre el tema.



Saludos.



PD. Os advierto que he acabado con esto, pero más adelante seguiré con los círculos del altura iguales.

[Keith11]

me lo bajo, pero ya

Originalmente publicado por MasBarco

PD. Os advierto que he acabado con esto, pero más adelante seguiré con los círculos del altura iguales.

¡¡¡ no hay huevos!!!

[capitan tan]

Gracias, monstruo. Muy muy interesante

[havgan]

Muy currado el tema de la navegación astronomica, me lo guardo para cuando me toque estudiarlo. Lo cierto es que casi no entiendo un pijo pero es estupendo ver como hay cofrades que no dudan en mostrar sus conocimientos para el beneficio comun.Lo dicho una currada Tropelio.Saludos y birras.
Nos vemos en los mares

[Mascocó]

Gracias capitan tan y Keith11 por vuestras apreciaciones, aunque sinceramente tengo que decir que me desanima un tanto que haya tenido tan poco eco mi aportación.

En cualquier caso Keith11, claro que voy a sacar la hoja sobre los círculos de altura, en realidad es bastante más sencilla que toda la liada anterior, ya estoy preparando los dibujitos dichosos, que es lo que más tiempo se lleva, espero acabarlo esta tarde o si no mañana mismo.


Saludos cordiales.

[capitan tan]

Originalmente publicado por MasBarco

Gracias capitan tan y Keith11 por vuestras apreciaciones, aunque sinceramente tengo que decir que me desanima un tanto que haya tenido tan poco eco mi aportación.

No, masbarco, no te desanimes. Es imposible llegar a apreciar a veces algunas de las curradas que se ha pegado alguien. Sobre todo en temas muy específicos y concretos como este. Gracias otra vez y quedo a la espera de tu siguiente entrega

[Mascocó]

Como lo prometido es deuda, aunque con un poco de retraso, MasBarco ataca de nuevo.

Pués bien, como la cuestión de las iteraciones no me convencía demasiado con la historia de los puntos de no convergencia, o los que pueden necesitar 25 o más iteraciones (imaginaros los cálculos con calculadora), y el método de Círculos de altura iguales tiene el aliciente de que, en principio, no se necesita ninguna situación de estima, he hecho el mismo trabajo que para las iteraciones, es decir meter los cálculos necesarios en una hoja de cálculo para que ésta nos ahorre el trabajo de resolver manualmente (con ayuda de calculadora se supone) los tres triángulos esféricos.

Siguiendo las sumamente claras explicaciones de Tropelio, ésta es la hoja de cálculo que sigue su metodología: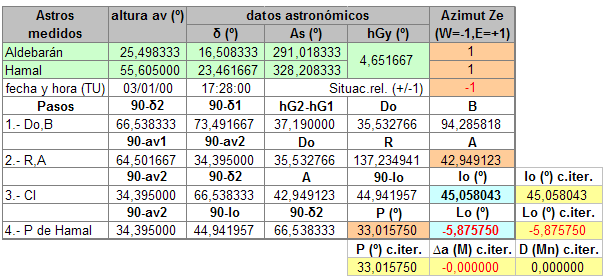



Esta hoja es bastante sencilla, mucho más que la de iteraciones, en las que hay que calcular el cruce de dos rectas, apartamientos etc…, aunque luego se complica un tanto si queremos automatizar al máximo la obtención de resultados.

Al igual que en el caso de las iteraciones, basta en principio con introducir los datos astronómicos y la altura verdadera de los astros observados (recuadros en verde). Luego explicaré qué son los datos de la columna de azimut. Los resultados de posición aparecen con fondo azul y el ángulo en el polo obtenido corresponderá al astro que tomamos como “Astro2”, el de la segunda fila de datos.

Las filas y columnas en amarillo en realidad no forman parte de la hoja de cálculo para los círculos de altura, corresponden a los resultados de iteración para una situación de estima aproximada (+1º el lat. y Lon.) a la obtenida por el método de círculos de altura.

En este caso del ejemplo de Aldebarán/Hamal que puso Tropelio, como se puede ver, se obtiene el mismo resultado que en su cálculo y también el mismo que por el método de iteraciones.

Pero veamos qué pasa si aplicamos tal cual estas fórmulas a una de las otras observaciones que hemos tratado en las iteraciones, concretamente a la de Mimosa y Denébola:



Como se puede ver, el resultado no corresponde a ninguno de los dos posibles puntos de observación, mientras que el resultado por el método de iteración converge a la primera de las dos posibles situaciones de observación.

La razón es bien sencilla, el método de cálculo no se puede aplicar a ojos cerrados ya que el cálculo del ángulo A y el signo del ángulo en el polo P dependen de nuestra situación relativa respecto a los dos astros observados.



Continúo en el siguiente post.

[Mascocó]

Veamos cuales son las cuatro posibles combinaciones de las situaciones relativas entre nuestro punto de observación y los astros observados.

Con los dos astros al este del supuesto punto de observación los triángulos esféricos se plantean como: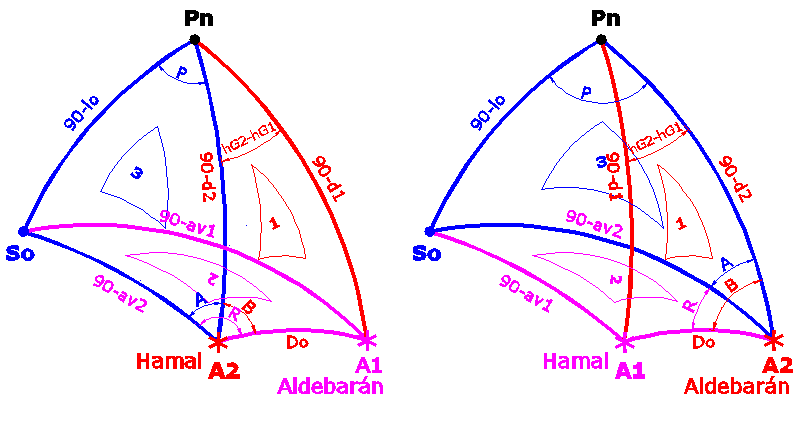



(planteo en cada caso dos figuras para tomar en cuenta que se invierta el orden de los dos astros en los cálculos. Los triangulos pequeños numerados del 1 al 3 intentan indicar el orden de resolución de los triángulos esféricos.)

Este caso, concretamente la figura de la izquierda, corresponde al planteado por Tropelio en su explicación.

Aquí, como perfectamente explicó Tropelio, A= (R-B) y el ángulo en el polo es E (positivo) y corresponde al de Hamal. Aclaro que solo considero el valor absoluto los ángulos A, B y R, a efecto de los cálculos podemos considerarlos todos en valor absoluto, lo que si importa es tener en cuenta el signo del ángulo en el polo P a la hora de calcular la longitud de observación.

En el de la derecha, A= (B-R)= -(R-B) y el ángulo en el polo será el correspondiente a Aldebarán pero en todo caso también E.

Si supusiéramos esta misma situación relativa para Mimosa/Denébola el resultado sería el erróneo que hemos obtenido, en realidad el problema es que nuestra situación relativa con Mimosa/Denébola es la siguiente: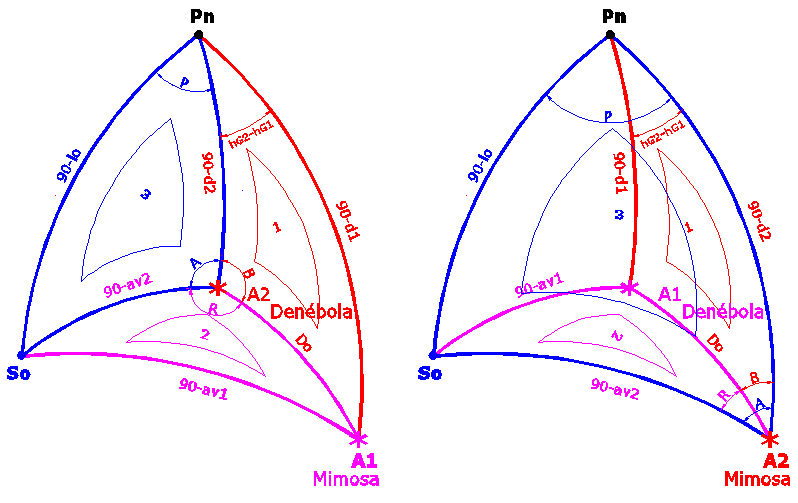



Donde A= 360-(R+B)]= -(R+B) (izquierda) o A= +(R+B) (derecha) y los ángulos en el polo E. En los dos casos P es E.

Es decir el ángulo A hay que calcularlo como (R+B) en lugar de, como en el caso anterior, como (R-B).

Esto claramente es debido a que nuestra situación relativa está, digamos, por debajo de uno de los astros, o a que uno de los astros queda en medio de nuestra situación y del otro astro, como querais.

Los otros dos casos que se pueden dar es cuando tenemos un astro a cada lado.

Caso de Alphecca/Capella: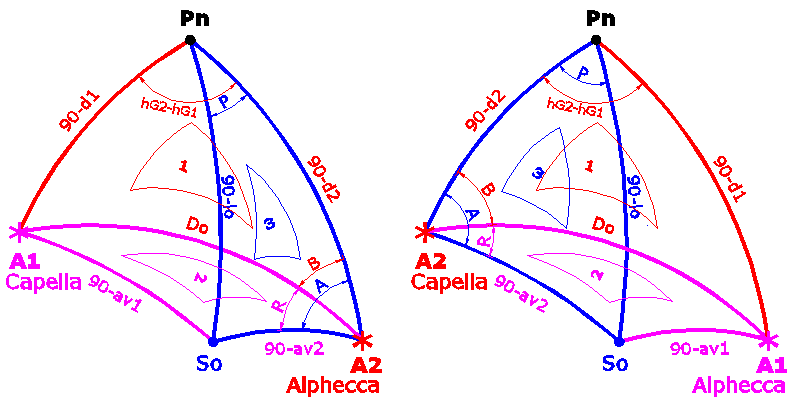



Donde A= +(R+B) (izquierda) y A= +(R+B) (derecha) y los ángulos en el polo, el de Alphecca E y el de Capella W.

El último caso: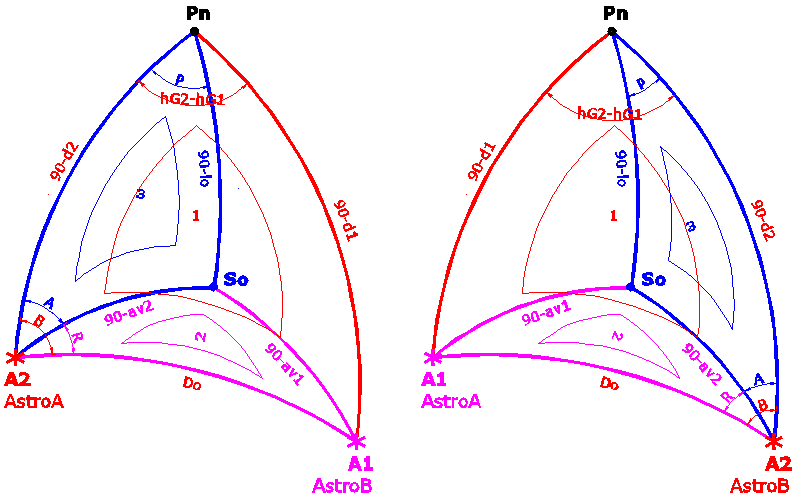



En el que A= B-R= -(R-B) (izquierda) y A= B-R= -(R-B) (derecha) y los ángulos en el polo contrarios en signo. De nuevo, la cuestión respecto al ángulo A consiste en calcularlo como (R+B) o como (R-B).

Desde luego hay más casos, cuando los dos astros están al Oeste en lugar de al Este de nuestra posición, pero a efectos prácticos se reducen a los presentados




Continúo en el siguiente post.

[Mascocó]

Resumiendo, no es completamente cierto lo de sin situación de estima, la realidad es que no vale cualquier situación de estima sino que tenemos que aproximarla por nuestra situación relativa a los astros observados.

Tampoco es que represente mayor problema, claro, basta con saber si los astros están los dos a nuestro E, a nuestro W o uno a cada lado, cosa bastante fácil. Un poco más difícil, al menos en alguna de las situaciones que se pueden dar, es saber si alguno o los dos astros están por encima o por debajo de nuestra latitud. Si estamos resolviendo el problema de manera manual normalmente nos haremos un dibujo de planteamiento, situando más o menos los astros respecto a nosotros (que al fin y al cabo representa suponer una cierta posición de estima), con lo que el valor de A y P ya lo calcularemos correctamente.

Para resolver el problema de manera automática tenemos que suministrarle a la hoja de cálculo, que no es tan lista como nosotros, esta información. Se lo diremos en la columna Azimut, en las dos primeras filas introduciendo el signo del azimut del astro respecto a nuestra situación prevista, -1 si está a nuestro W ó +1 si está al E de nuestra posición y en la tercera, la de situación relativa, con un +/-1 según supongamos estar por encima o no. De ahí los fondos de las cuadrículas en marrón, que puse así para resaltar la relación de cálculo entre ellas.

Una cosa que puede ayudarnos para discernir los resultados correctos, es que, para un caso dado de supuesta situación relativa, los resultados deben ser los mismos si intercambiamos un astro por el otro, y, cuando no hemos acertado con la posición relativa correcta los resultados son diferentes.

Por ejemplo, para el último caso que hemos visto de Mimosa/Denébola, en la que tenemos mal la posición relativa, si intercambiamos Mimosa por Denébola en los cálculos, resulta: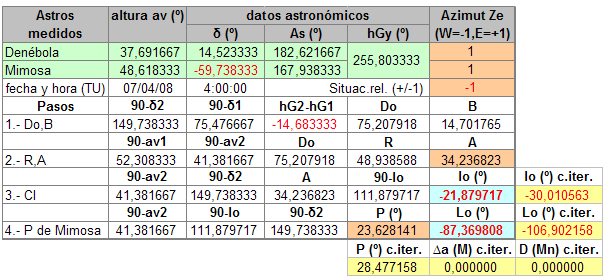




Dando un resultado de posición, también erróneo por supuesto, y, lo que nos importa, diferente al anterior.

Es decir, que intercambiando los astros, para una cierta supuesta situación relativa, los resultados sólo serán iguales para las dos posiciones correctas.

En el caso Mimosa/Denébola una de estas posiciones es: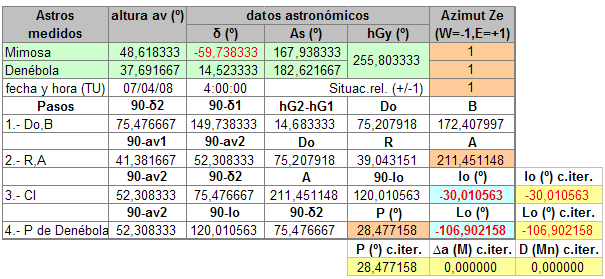




y la otra: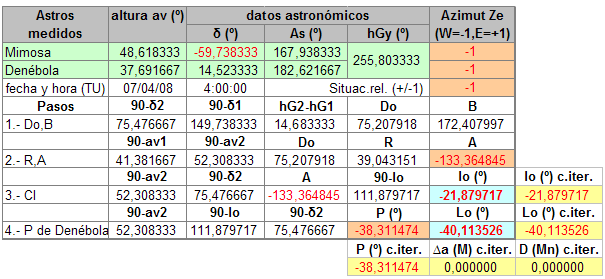




La otra correcta de Aldebarán/Hamal:



Resultados que, como era de esperar dando posiciones relativas correctas, coinciden con los de iteración.




Continúo en el siguiente post.

[Mascocó]

Con todo lo anterior ya podemos completar una hoja de cálculo que contemple los casos posibles y nos filtre los correctos. Independientemente de que, si le hemos suministrado la posición relativa correcta nos dé directamente nuestra situación.

Esta hoja queda así: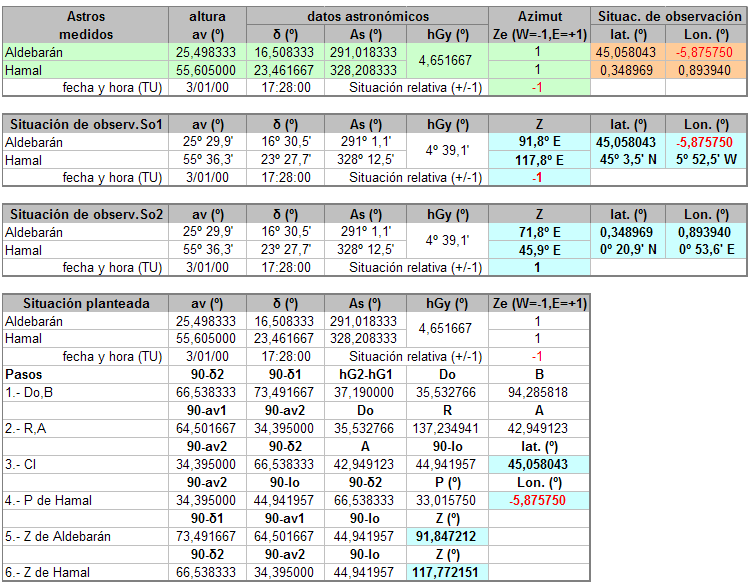




No hay mas que rellenar los datos en verde y la hoja calcula las dos posiciones de observación y los azimutes a los astros, dando como posición So1 la real nuestra si la estimación de posición relativa es correcta. En el cuadro Situación planteada se presentan los cálculos completos correspondientes a los suministrados como posición relativa, dando los resultados de posición y azimut con fondo azul si son correctos y cambiando el color de fondo en caso contrario.

Al igual que en el caso de la hoja de cálculo por iteraciones, los datos de Situación de observación con fondo marrón y los de fecha y hora (TU) son meramente informativos.




Continúo en el siguiente post.

[Mascocó]

Un par de ejemplos más.

Observaciones de Mimosa y Denébola con situación relativa errónea: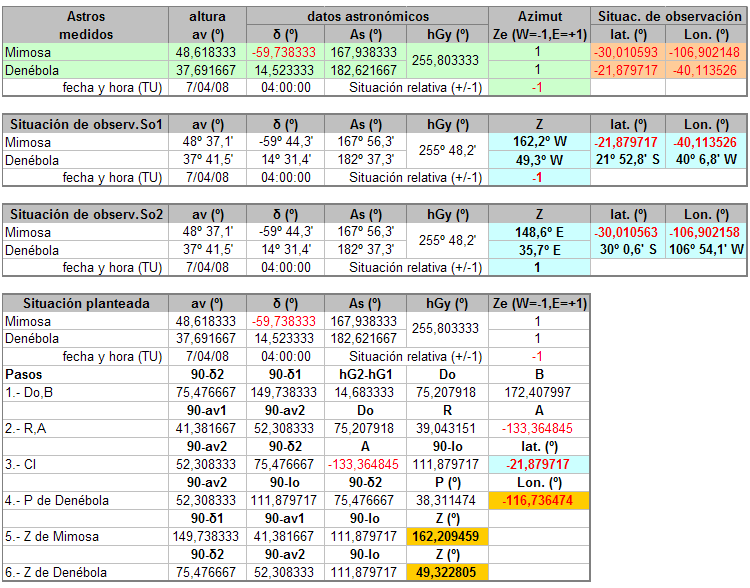




Como se ve, la hoja calcula igualmente las dos posibles situaciones pero, al ser errónea nuestra situación planteada, destaca en el cuadro inferior, con fondo amarillo, los resultados erróneos.

Y, por último:

Observaciones de Alphecca y Capella con situación relativa correcta: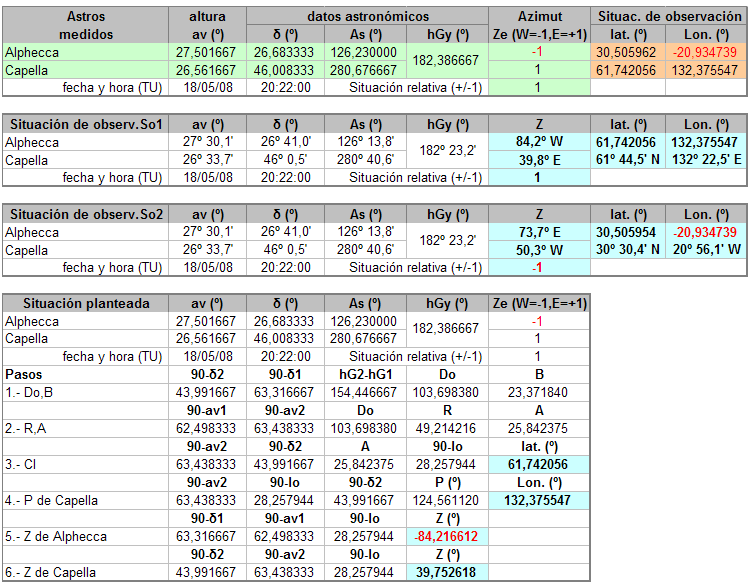







Y ya, termino en el siguiente post.

[Mascocó]

Quería comentar por último que soy consciente de que toda esta cuestión de círculos de altura iguales puede resolverse mediante un programita en casi cualquier lenguaje, probablemente de manera mucho más sencilla que a través de la hoja de cálculo que planteo, pero por otro lado pienso que de esta manera se ven y se pueden seguir más claramente los pasos intermedios, que así pueden ser más accesibles para gente sin conocimientos de programación.

Adjunto la hoja de cálculo que es un fichero en Excel que podeis descargar al final del post desde Archivos adjuntos.



Agradecería que me comunicarais los errores que podais encontrar, así como cualquier comentario o sugerencia.



Saludos.


PD. Inicialmente había puesto el fichero .xls solo como adjunto porque creía poder actualizarlo posteriormente, pero no es así (solo durante el periodo de edición), así que adjunto un enlace al mismo fichero, que, aunque tiene que estar en formato .zip, ocupa menos espacio. Aprovecho para añadir alguna mejora menor (como revisión de los datos introducidos). De momento también lo dejo como adjunto (actualizado como versión v1.1) pero si lo tengo que borrar y no podeis descargarlo de ahí podreis hacerlo desde:

CA Circulos de altura iguales (v11).xls


También incorporo aquí un enlace directo a la otra hoja de cálculo, la de iteraciones, ya que ya no puedo hacerlo desde el mensaje donde está el adjunto:

CA Iteraciones (MasBarco v10).xls

Disculpad.

[Keith11]

Originalmente publicado por MasBarco

Quería comentar por último que soy consciente de que toda esta cuestión de círculos de altura iguales puede resolverse mediante un programita en casi cualquier lenguaje, probablemente de manera mucho más sencilla que a través de la hoja de cálculo que planteo, pero por otro lado pienso que de esta manera se ven y se pueden seguir más claramente los pasos intermedios, que así pueden ser más accesibles para gente sin conocimientos de programación.



Adjunto la hoja de cálculo que es un fichero en Excel que podeis descargar al final del post desde Archivos adjuntos.



Agradecería que me comunicarais los errores que podais encontrar, así como cualquier comentario o sugerencia.



Saludos.

MasBarco

... no he entrado a fondo en tus posts, pero ya te felicito por la currada, y por el sentilo del analisis que destilas... así como tu gusto por la "comida de olla"

Te aseguro que me lo leere... tengo ganas de retomar mi gusto por la navegacion astronomica

Saludos y agradecido por tu esfuerzo... ¡te debo una!!!

... y me bajo la excel esa para meterla en algun aparetejo diabolico de esos modelnos...

[Mascocó]

Gracias Keith, pero no te entiendo, la comida de olla no me gusta demasiado, excepto los spaghettis y demás prefiero los fritos y las cosas a la brasa.

Pero tienes razón, si me hubiera limitado a las primeras hojas de cálculo, para andar por casa, que preparé, todo esto me hubiera llevado muucho menos tiempo, la comedura de coco (cocolla se me ocurriría llamarlo) empieza cuando se te ocurre presentarlo en público, y con el nivel que hay en este foro... pues pasa eso, que viene la cocolla.


Un saludo

Originalmente publicado por MasBarco

Resumiendo, no es completamente cierto lo de sin situación de estima, la realidad es que no vale cualquier situación de estima sino que tenemos que aproximarla por nuestra situación relativa a los astros observados.

Tampoco es que represente mayor problema, claro, basta con saber si los astros están los dos a nuestro E, a nuestro W o uno a cada lado, cosa bastante fácil. Un poco más difícil, al menos en alguna de las situaciones que se pueden dar, es saber si alguno o los dos astros están por encima o por debajo de nuestra latitud. Si estamos resolviendo el problema de manera manual normalmente nos haremos un dibujo de planteamiento, situando más o menos los astros respecto a nosotros (que al fin y al cabo representa suponer una cierta posición de estima), con lo que el valor de A y P ya lo calcularemos correctamente.

Para resolver el problema de manera automática tenemos que suministrarle a la hoja de cálculo, que no es tan lista como nosotros, esta información. Se lo diremos en la columna Azimut, en las dos primeras filas introduciendo el signo del azimut del astro respecto a nuestra situación prevista, -1 si está a nuestro W ó +1 si está al E de nuestra posición y en la tercera, la de situación relativa, con un +/-1 según supongamos estar por encima o no. De ahí los fondos de las cuadrículas en marrón, que puse así para resaltar la relación de cálculo entre ellas.

Una cosa que puede ayudarnos para discernir los resultados correctos, es que, para un caso dado de supuesta situación relativa, los resultados deben ser los mismos si intercambiamos un astro por el otro, y, cuando no hemos acertado con la posición relativa correcta los resultados son diferentes.

Por ejemplo, para el último caso que hemos visto de Mimosa/Denébola, en la que tenemos mal la posición relativa, si intercambiamos Mimosa por Denébola en los cálculos, resulta:




Dando un resultado de posición, también erróneo por supuesto, y, lo que nos importa, diferente al anterior.

Es decir, que intercambiando los astros, para una cierta supuesta situación relativa, los resultados sólo serán iguales para las dos posiciones correctas.

En el caso Mimosa/Denébola una de estas posiciones es:




y la otra:




La otra correcta de Aldebarán/Hamal:



Resultados que, como era de esperar dando posiciones relativas correctas, coinciden con los de iteración.




Continúo en el siguiente post.

Hola MasBarco,

Bueno, tremendo curro te has metido con las hojas de cálculo estas. Yo no sé utilizar ese programa, así que no puedo opinar sobre el asunto.

Lo que sí me gustaría comentar es que no estoy de acuerdo con lo que dices de que no es completamente cierto que puedas calcular tu situación sin tener en absoluto idea de situación de estima alguna. Es evidente que se puede pues arriba, al comienzo del hilo, yo lo he hecho con una simple calculadora. Si esto se intenta poner en práctica, midiendo las alturas de dos astros, está claro que cualquier navegante que lo haga anotará no sólo las alturas y las horas sino, también, por donde ve cada uno de los astros (o sea, si su azimut es este u oeste). Eso basta para resolver completamente el problema y no tiene nada que ver con tener una situación de estima. O sea, que SI es perfectamente posible situarse con dos observaciones astronómias sin tener idea alguna de dónde estás.

Otra cosa diferente es pretender "automatizar" el asunto. Ahí, claro, tienes que tener en cuenta que, como muy bien dices, los programas de ordenador son muchísimo menos inteligentes que los humanos que los crean. Pero esto no es nada sorprendente: una simple arcotangente con una vulgar calculadora te puede jugar una mala pasada calculando el azimut de un astro si no eres más inteligente que la calculadora y tienes en cuenta que el arcotangente es una función de muy mala familia pues hay dos ángulos con el mismo valor de la tangente... O sea que no me sorprende que cuando quieres automatizar lo que proponía arriba de este hilo te encuentres con desagradables sorpresas...

Un cordial saludo,
Tropelio

[Mascocó]

Hola Tropelio,

Vaya, díficil es contradecirte, porque seguramente al final tendrás razón pero trataré de explicar lo que quiero decir.

Estrictamente hablando es cierto que no necesitas ninguna posición de estima, de hecho la hoja de cálculo finalmente no utiliza ninguna, pero sí necesitas saber tu posición relativa respecto a los astros para dibujar correctamente los triángulos esféricos y plantear bien el cálculo del ángulo A como (R-B) o (R+B).

Está claro que, como ya dije, el situar los astros a tu E o W no tiene problema, pero según supongas tu latitud y según sean las codeclinaciones de los astros te sale un dibujo u otro, cambiando el cálculo del ángulo A.

Si te fijas en el ejemplo que puse de Mimosa y Denébola verás que la resolución correcta implica dibujar los tres triángulos digamos externos, no entrelazados, como en el caso de Aldebarán y Hamal, si supones una latitud para tu posición más al norte de las dos posibles te sale el mismo dibujo de tu ejemplo... y resultados erróneos. Eso si el que no está errado soy yo, claro.

Y me da la impresión de que exclusivamente con las medidas de los astros, si no haces una cierta estima de tu latitud, puede ser que no obtengas a la primera el resultado correcto.

No sé si me he explicado bien, quizás con la ayuda de los dibujos de los triángulos lo hice mejor. O quizás hasta esté completamente equivocado.


Gracias de nuevo por tus explicaciones, sin las cuales mis deducciones ni se habrían iniciado.

Un saludo

[zascandil]

Hola a todos

Muchas rondas a todo el personal que un post como este las merece.

Me acabo de volver a registrar después de muchiiiisimo tiempo sin entrar en este antro tabernario (mi antiguo nick no funciona) y me encuentro con este post excelente del Maestro Tropelio. Ya tuvimos una discusión similar sobre el método de los círculos de altura hace mucho tiempo en esta misma Taberna con otros tabernarios ilustres de los que aprendí mucho. Veo que el nivelazo del foro es ahora, si cabe, mayor.

Tropelio, es impresionante la facilidad que tienes para explicar cosas de manera sencilla y amena. Gracias por acordarte de servidora. Tómate una barrica de ron a cuenta de los ratos que hemos pasado discutiendo la vacilada esa de hacer respirar los círculos de altura.

Pacoperas, recibe un cordialísimo saludo que hace más de veinte años que no nos hemos vuelto a ver, creo que fue en el `86, pero con este post he vuelto a saber de ti. Veo que además de un guru de los GigaHz en su día, lo eres ahora también de los astros y su historia. No conocía el libro ese y lo voy tener que encargar porque hace muy poco Tropelio también me hablo de él.

Masbarco, es acojonante la claridad y orden de tus hojas de cálculo y los análisis que has hecho. Es realmente un trabajo excelente y que me bajo porque me va a ser muy útil. Por eso lamento contradecirte y darle la razón a Tropelio (y sin que sirva de precedente) cuando dices que realmente hace falta una cierta “estima” para resolver. El problema es que al automatizar el calculo hay que saber decirle a la máquina como obtener los signos del calculo de los ángulos. Esto es posible programarlo a partir de las posiciones relativas de los astros y del tamaño de las alturas. Pero para una hoja de cálculo Excel es mucho más sencillo proceder a lo “bruto” calculando todas las soluciones posibles, es decir todas las combinaciones de signos y luego seleccionar las dos únicas soluciones que cumplen el requisito de estar a una distancia 90-av de cada uno de los dos astros.

Naturalmente el método de los círculos de alturas que ha explicado brillantemente Tropelio da dos resultados. Si usamos tres astros y aplicamos el mismo método solo habrá una única solución, habiendo eliminado además los posible errores sistemáticos en la toma de alturas.

Y ahora una pregunta,...a ver,... ¿qué pasa si no tenemos compás de marcaciones o no podemos medir el azimut del astro por estar éste muy alto?¿cómo podemos entonces situarnos SIN ESTIMA si las observaciones no son simultáneas?,...y no, no vale sacar el GPS.

Venga, más rondas del mejor Macallan Fine & Rare para todos.

Zascandil

[Mascocó]

Originalmente publicado por zascandil

Masbarco...
... Por eso lamento contradecirte y darle la razón a Tropelio (y sin que sirva de precedente) cuando dices que realmente hace falta una cierta “estima” para resolver. El problema es que al automatizar el calculo hay que saber decirle a la máquina como obtener los signos del calculo de los ángulos. Esto es posible programarlo a partir de las posiciones relativas de los astros y del tamaño de las alturas. Pero para una hoja de cálculo Excel es mucho más sencillo proceder a lo “bruto” calculando todas las soluciones posibles, es decir todas las combinaciones de signos y luego seleccionar las dos únicas soluciones que cumplen el requisito de estar a una distancia 90-av de cada uno de los dos astros.

Bueno zascandil, más que gracias por tu estimación, máxime por situarme al lado de cofrades como Tropelio y Pacoperas, cosa que no merezco ni de c... Y lo digo en serio, sin falsa modestia.

En cuanto a lo de hacer falta o no cierta estima tengo que insistir, con el riesgo de equivocarme una vez más. Cuando resuelves el problema manualmente te harás un planteamiento de los triángulos esféricos; para colocarlos a tu derecha o izquierda no necesitas nada más que haber tomado nota al observarlos, pero, según dibujes tu supuesta colatitud, te saldrá un sistema de triángulos u otro y por tanto una resolución de los ángulos u otra, solo uno de los resultados es el correcto. Por eso digo, lo que por otra parte para nada desmerece, ni quiere desmerecer, el método de círculos de altura iguales planteado por Tropelio, que hace falta una cierta estima en latitud. Resuelve el problema que plantea Tropelio de Aldebarán/Hamal con So dibujada en el hemisferio sur, o el de Mimosa/Denébola con So en el norte y verás lo que quiero decir. En el momento que obtienes un resultado diferente según pongas tu supuesta latitud más al norte o al sur de un determinado punto, digo yo que estarás haciendo una cierta estima, aunque no pongas cifras. Pero, en fin, que al final igual es solo una cuestión semántica y tampoco quisiera insistir más en el asunto.

Como podrás ver, en la hoja de cálculo que planteo efectivamente se utiliza la fuerza bruta, aunque sólo calcula las ocho situaciones posibles rechazando el resultado si, invirtiendo el orden de los astros (lo que al final hace 16 resoluciones, jeje), no se obtienen los mismos resultados en latitud y longitud. El decirle a la hoja tu posición relativa, al final es anecdótico, la hoja calcula igualmente las dos posibles soluciones.

Lo de tus "círculos respirados" ya es el colmo , he empezado a mirarlo a fondo y, si puedo, trataré de hacer también una hoja de cálculo que los incluya, para cuando las observaciones no sean simultáneas.

Lo de los tres círculos y lo de "sin azimut" que planteas ya es para nota, yo, de momento me conformo con el aprobado.


Saludos cordiales

[pacoperas]

Originalmente publicado por zascandil

Pacoperas, recibe un cordialísimo saludo que hace más de veinte años que no nos hemos vuelto a ver, creo que fue en el `86, pero con este post he vuelto a saber de ti. Veo que además de un guru de los GigaHz en su día, lo eres ahora también de los astros y su historia. No conocía el libro ese y lo voy tener que encargar porque hace muy poco Tropelio también me hablo de él.

Me has dejado descolocado.Debe ser cosa de los años, que el cerebro lo tengo lleno de agujeros.

Veo que eres de los pocos que saben de mis antiguas actividades subiendo a los montes con la parabolilla para hacer contactos en 10 GHz. Pero, la verdad, no te asocio a una persona en particular, ya me contarás donde y cuando nos vimos.

Recibe tu también un cordialísimo saludo,

Salud y buenos vientos

[Avante]

Gracias por este tema tan interesante

Si tuviera que resolver este caso de "caída en medio del mar en paracaídas con una calculadora, un cronómetro, el almanaque y un sextante" se me habría ocurrido otro método que es mucho menos elegante pero creo que - corrígeme si me equivoco- más o menos preciso.

El apaño consistiría en calcular con meridiana y circunmeridiana latitud y longitud: la primera sería prácticamente exacta; la segunda no tanto, aunque entiendo que sí lo suficiente para dar una situación de estima. Aprovechando esa situación de estima y la meridiana tomaría una segunda lectura al ocaso, con la que corregir la Se hallada hace unas horas y conseguir una posición entiendo que exacta.

¿Funcionaría este método?

Saludos

Avante

Originalmente publicado por Avante

Gracias por este tema tan interesante

Si tuviera que resolver este caso de "caída en medio del mar en paracaídas con una calculadora, un cronómetro, el almanaque y un sextante" se me habría ocurrido otro método que es mucho menos elegante pero creo que - corrígeme si me equivoco- más o menos preciso.

El apaño consistiría en calcular con meridiana y circunmeridiana latitud y longitud: la primera sería prácticamente exacta; la segunda no tanto, aunque entiendo que sí lo suficiente para dar una situación de estima. Aprovechando esa situación de estima y la meridiana tomaría una segunda lectura al ocaso, con la que corregir la Se hallada hace unas horas y conseguir una posición entiendo que exacta.

¿Funcionaría este método?

Saludos

Avante

Ummm, pues yo creo que no porque en caso de "caída en medio del mar en paracaídas con una calculadora, un cronómetro, el almanaque y un sextante"
lo más probable es que el almanaque y la calculadora se te fueran al garete mojados por el agua de mar....

no lo he podido evitar...

Saludos,
Tropelio

Originalmente publicado por zascandil

Hola a todos

Muchas rondas a todo el personal que un post como este las merece.

Me acabo de volver a registrar después de muchiiiisimo tiempo sin entrar en este antro tabernario (mi antiguo nick no funciona) y me encuentro con este post excelente del Maestro Tropelio. Ya tuvimos una discusión similar sobre el método de los círculos de altura hace mucho tiempo en esta misma Taberna con otros tabernarios ilustres de los que aprendí mucho. Veo que el nivelazo del foro es ahora, si cabe, mayor.

Tropelio, es impresionante la facilidad que tienes para explicar cosas de manera sencilla y amena. Gracias por acordarte de servidora. Tómate una barrica de ron a cuenta de los ratos que hemos pasado discutiendo la vacilada esa de hacer respirar los círculos de altura.

Pacoperas, recibe un cordialísimo saludo que hace más de veinte años que no nos hemos vuelto a ver, creo que fue en el `86, pero con este post he vuelto a saber de ti. Veo que además de un guru de los GigaHz en su día, lo eres ahora también de los astros y su historia. No conocía el libro ese y lo voy tener que encargar porque hace muy poco Tropelio también me hablo de él.

Masbarco, es acojonante la claridad y orden de tus hojas de cálculo y los análisis que has hecho. Es realmente un trabajo excelente y que me bajo porque me va a ser muy útil. Por eso lamento contradecirte y darle la razón a Tropelio (y sin que sirva de precedente) cuando dices que realmente hace falta una cierta “estima” para resolver. El problema es que al automatizar el calculo hay que saber decirle a la máquina como obtener los signos del calculo de los ángulos. Esto es posible programarlo a partir de las posiciones relativas de los astros y del tamaño de las alturas. Pero para una hoja de cálculo Excel es mucho más sencillo proceder a lo “bruto” calculando todas las soluciones posibles, es decir todas las combinaciones de signos y luego seleccionar las dos únicas soluciones que cumplen el requisito de estar a una distancia 90-av de cada uno de los dos astros.

Naturalmente el método de los círculos de alturas que ha explicado brillantemente Tropelio da dos resultados. Si usamos tres astros y aplicamos el mismo método solo habrá una única solución, habiendo eliminado además los posible errores sistemáticos en la toma de alturas.

Y ahora una pregunta,...a ver,... ¿qué pasa si no tenemos compás de marcaciones o no podemos medir el azimut del astro por estar éste muy alto?¿cómo podemos entonces situarnos SIN ESTIMA si las observaciones no son simultáneas?,...y no, no vale sacar el GPS.

Venga, más rondas del mejor Macallan Fine & Rare para todos.

Zascandil

Coño!, el mismísimo Zascandil! Bienvenido hombre. ¿Ves como no pasaba nada? estos piratones no son tan malos como aparentan y no te comerán a pesar de ser el armador de un flamante Bavaria! (bueno, si lo fueses de un MacGregor la cosa sería seguramente muy distinta...). Me alegro un güevo de leerte por aquí, ganaremos todos un montón con tus aportaciones.

Y ya veos que empiezas duro. A ver que aprendemos del asunto de respirar los círculos de altura sin siquiera medir el azimut... Estoy en ascuas.

Un abrazo,
Tropelio